题目内容
8．如图是一个几何体的三视图，则该几何体的表面积为33π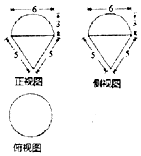
分析 由几何体的三视图得出该几何体是半球体与圆锥体的组合体，
结合图中数据求出组合体的表面积即可．
解答 解：由几何体的三视图可得：
该几何体是半球体与圆锥体的组合体，
且圆锥底面与半球圆面重合，
该组合体的表面积为：
S=S半球面+S圆锥侧面=2π×32+π×3×5=33π．
故答案为：33π．
点评 本题考查了几何体三视图的应用问题，是基础题目．
练习册系列答案
相关题目
18．已知圆O的半径为1，A，B，C，D为该圆上四个点，且$\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}$，则△ABC的面积最大值为（ ）
| A． | 2 | B． | 1 | C． | $\sqrt{2}$ | D． | $\sqrt{3}$ |
19．圆：x2+y2+2ax+a2-9=0和圆：x2+y2-4by-1+4b2=0有三条公切线，若a∈R，b∈R，且ab≠0，则$\frac{4}{a^2}+\frac{1}{b^2}$的最小值为（ ）
| A． | 1 | B． | 3 | C． | 4 | D． | 5 |
3．函数y=sin2x的图象向左平移φ（φ＞0）个单位后关于直线$x=\frac{π}{3}$对称，则φ的最小值为（ ）
| A． | $\frac{π}{12}$ | B． | $\frac{5π}{12}$ | C． | $\frac{π}{6}$ | D． | $\frac{5π}{6}$ |
13．若复数z满足（1+i）z=2-i（i为虚数单位），则|z|=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{10}}}{2}$ | C． | 2 | D． | $\frac{{3\sqrt{2}}}{2}$ |
17．若将函数y=2cos2x的图象向右平移$\frac{π}{12}$个单位长度，则平移后图象的一个对称中心为（ ）
| A． | （$\frac{5}{6}$π，0） | B． | （$\frac{7π}{6}$，0） | C． | （-$\frac{π}{3}$，0） | D． | （$\frac{π}{6}$，0） |
18．五个人围坐在一张圆桌旁，每个人面前放着完全相同的硬币，所有人同时翻转自己的硬币．若硬币正面朝上，则这个人站起来； 若硬币正面朝下，则这个人继续坐着．那么，没有相邻的两个人站起来的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{15}{32}$ | C． | $\frac{11}{32}$ | D． | $\frac{5}{16}$ |