题目内容

已知复数z满足（1+
3
i）z=1+i，则|z|=（　　）
A、
2
2
B、
1
2
C、
2
D、2
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：利用复数代数形式的乘除运算化简求出z，然后直接代入复数模的公式求解．
解答： 解：∵（1+
3
i）z=1+i，
∴z=
1+i
1+
3
i
=
(1+i)(1-
3
i)
(1+
3
i)(1-
3
i)
=
1+
3
+i-
3
i
4
=
1+
3
4
+
1-
3
4
i．
∴|z|=
(
1+
3
4
)2+(
1-
3
4
)2
=
2
2
．
故选：A．
点评：本题考查了复数代数形式的乘除运算，考查了复数模的求法，是基础题．
练习册系列答案
相关题目
在△ABC中，内角A、B、C所对的边分别为a，b，c，已知tanB=
1
2
，tanC=
1
3
，且c=1．
（Ⅰ）求tanA；
（Ⅱ）求a值．
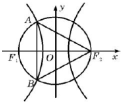如图，F1、F2分别是双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的两个焦点，以坐标原点O为圆心，|OF1|为半径的圆与该双曲线左支交于A、B两点，若△F2AB是等边三角形，则双曲线的离心率为 （　　）
A、
3
B、2
C、
3
-1
D、1+
3
已知全集U=R，集合A={x|x＞4}，B={x|-6＜x＜6}
（1）求A∩B；
（2）求∁RB；
（3）定义A-B={x|x∈A，x∉B}，求A-B，A-（A-B）
在数列{an}中a1=1，当n≥2时，其前n项和Sn满足Sn（Sn-an）+2an=0．
（1）证明数列{
1
Sn
}是等差数列；
（2）求Sn和数列{an}的通项公式an；
（3）设bn=
1
Sn
•2n+1，求数列{bn}的前n项和Tn．
下列函数中，与函数y=
1
x
+
1
1-x
有相同定义域的是（　　）
A、f（x）=lnx+1g（1-x）
B、f（x）=
x
+
1-x
C、f（x）=
1
x(x-1)
D、f（x）=ex
若函数f（x）=
ax-2
在[2，+∞）上有意义，则实数a的取值范围为（　　）
A、a=1B、a＞1
C、a≥1D、a≥0
若抛物线y2=2px的准线与双曲线
x2
a2
-
y2
b2
=1（a，b＞0）的渐近线构成有一个内角120°的三角形，则双曲线的离心率为（　　）
A、
2
3
3
B、
2
C、
3
D、2
已知f（x）=ax+
a-2
x
+2-2a（a＞0），若f（x）≥2lnx在[1，+∞）上恒成立，则a的取值范围是（　　）
A、（1，+∞）
B、[1，+∞）
C、（2，+∞）
D、[2，+∞）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网