题目内容
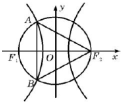 如图,F1、F2分别是双曲线
如图,F1、F2分别是双曲线| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
| B、2 | ||
C、
| ||
D、1+
|
考点:双曲线的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:连结AF1,根据圆的直径的性质和等边三角形的性质,证出△F1AF2是含有30°角的直角三角形,由此得到|F1A|=c且|F2A|=
c.再利用双曲线的定义,得到2a=|F2A|-|F1A|=(
-1)c,即可算出该双曲线的离心率.
| 3 |
| 3 |
解答:
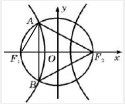 解:连结AF1,
解:连结AF1,
∵F1F2是圆O的直径,
∴∠F1AF2=90°,即F1A⊥AF2,
又∵△F2AB是等边三角形,F1F2⊥AB,
∴∠AF2F1=
∠AF2B=30°,
因此,Rt△F1AF2中,|F1F2|=2c,|F1A|=
|F1F2|=c,
|F2A|=
|F1F2|=
c.
根据双曲线的定义,得2a=|F2A|-|F1A|=(
-1)c,
解得c=(
+1)a,
∴双曲线的离心率为e=
=
+1.
故选D.
 解:连结AF1,
解:连结AF1,∵F1F2是圆O的直径,
∴∠F1AF2=90°,即F1A⊥AF2,
又∵△F2AB是等边三角形,F1F2⊥AB,
∴∠AF2F1=
| 1 |
| 2 |
因此,Rt△F1AF2中,|F1F2|=2c,|F1A|=
| 1 |
| 2 |
|F2A|=
| ||
| 2 |
| 3 |
根据双曲线的定义,得2a=|F2A|-|F1A|=(
| 3 |
解得c=(
| 3 |
∴双曲线的离心率为e=
| c |
| a |
| 3 |
故选D.
点评:本题给出以双曲线焦距F1F2为直径的圆交双曲线于A、B两点,在△F2AB是等边三角形的情况下求双曲线的离心率.着重考查了双曲线的定义、标准方程与简单几何性质等知识,属于中档题.

练习册系列答案
相关题目
若α∈(
,π),则2cos2α=sin(
-α),则sin2α的值为( )
| π |
| 2 |
| π |
| 4 |
A、
| ||
B、-
| ||
| C、1 | ||
D、
|
已知复数z满足(1+
i)z=1+i,则|z|=( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |