题目内容
6．已知f（x）=-3x2+a（6-a）x+b，若方程f（x）=0有一根小于1，另一根大于1，当b＞-6且b为常数时，求实数a的取值范围．分析 根据一元二次函数根的分布建立条件关系即可得到结论．
解答 解：∵f（x）=-3x2+a（6-a）x+b，
∴若方程f（x）=0有一根小于1，另一根大于1，
则f（1）＜0，
即-3+a（6-a）+b＜0，
即b＜a2-6a+3，
∵b＞-6且b为常数，
∴a2-6a+3＞-6，
即a2-6a+9＞0，
即（a-3）2＞0，
∴a≠3．
点评 本题主要考查一元二次函数根的分布，根据条件将方程根的问题转化为函数问题是解决本题的关键．
练习册系列答案
相关题目
15．
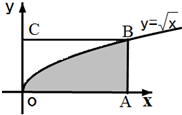如图，长方形的四个顶点为O（0，0），A（4，0），B（4，2），C（0，2），曲线$y=\sqrt{x}$经过点B，现将一质点随机投入长方形OABC中，则质点落在图中阴影区域的概率是（ ）
如图，长方形的四个顶点为O（0，0），A（4，0），B（4，2），C（0，2），曲线$y=\sqrt{x}$经过点B，现将一质点随机投入长方形OABC中，则质点落在图中阴影区域的概率是（ ）| A． | $\frac{2}{3}$ | B． | $\frac{3}{4}$ | C． | $\frac{4}{7}$ | D． | $\frac{7}{12}$ |
18．下列各项表示同一个函数的是（ ）
| A． | f（x）=$\frac{{x}^{2}-1}{x-1}$与g（x）=x+1 | B． | f（x）=$\sqrt{{x}^{2}}$-1与g（x）=x-1 | ||
| C． | f（x）=$\frac{（x+3）^{2}}{x+3}$，g（x）=（x+3）（x+3）0 | D． | f（x）=$\sqrt{-2{x}^{3}}$与g（x）=x$\sqrt{-2x}$ |