题目内容
16.求曲线y=log2x与曲线y=log2(4-x)以及x轴所围成的图形的面积.分析 首先画出曲线围成的图象,利用指数函数与对数函数的对称性将面积利用指数函数的定积分解答.
解答  解:曲线y=log2x与曲线y=log2(4-x)以及x轴所围成的图形的如图
解:曲线y=log2x与曲线y=log2(4-x)以及x轴所围成的图形的如图
两个曲线的交点是(2,1),关于y=x对称的图形如图,所以面积为${∫}_{0}^{1}(4-{e}^{x}-{e}^{x})dx$=(4x-2ex)|${\;}_{0}^{1}$=4-2e+2=6-2e.
点评 本题考查了利用等积法求曲线围成的面积;解答本题的关键是将所求转化为指数函数的等积法计算.

练习册系列答案
相关题目
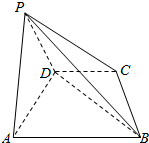 四棱锥P-ABCD中,△PAD为等边三角形,底面ABCD为等腰梯形,满足AB∥CD,AD=DC=$\frac{1}{2}$AB=2,且平面PAD⊥平面ABCD.
四棱锥P-ABCD中,△PAD为等边三角形,底面ABCD为等腰梯形,满足AB∥CD,AD=DC=$\frac{1}{2}$AB=2,且平面PAD⊥平面ABCD.