题目内容
求导数:f(x)=e2x.
考点:导数的运算
专题:导数的概念及应用
分析:根据函数的导数公式进行求解即可.
解答:
解:由于f(x)=e2x
则函数的导数为f′(x)=2e2x.
则函数的导数为f′(x)=2e2x.
点评:本题主要考查导数的计算,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)(x∈R)满足f′(x)>f(x),则( )
| A、f(1)>ef(0)>e2f(-1) |
| B、f(1)<ef(0)<e2f(-1) |
| C、e2f(-1)>ef(0)>f(1) |
| D、e2f(-1)<ef(0)<f(1) |
已知命题p:若a,b是任意实数,且a>b,则a2>b2,
命题q:若a,b是任意实数,且a>b,则(
)a<(
)b.
在命题①p∧q;②p∨q;③p∧(¬q);④(¬p)∨q中,
真命题的个数是( )
命题q:若a,b是任意实数,且a>b,则(
| 1 |
| 2 |
| 1 |
| 2 |
在命题①p∧q;②p∨q;③p∧(¬q);④(¬p)∨q中,
真命题的个数是( )
| A、1个 | B、2个 | C、3个 | D、4个 |
已知i为虚数单位,复数z满足i3•z=1-3i,则z的共轭复数是( )
| A、-3+i | B、-3-i |
| C、3-i | D、3+i |
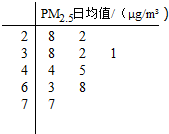 我国政府对PM2.5采用如下标准:
我国政府对PM2.5采用如下标准: 如图,已知Rt△ABC的两条直角边AC,BC的长分别为6cm,8cm,以AC为直径的圆与AB交于点D则BD=
如图,已知Rt△ABC的两条直角边AC,BC的长分别为6cm,8cm,以AC为直径的圆与AB交于点D则BD=