题目内容
1.若幂函数y=(m2-4m+1)xm2-2m-3为(0,+∞)上的增函数,则实数m的值等于4.分析 由函数y的幂函数得m2-4m+1=1,求出m的值,再由幂函数y在(0,+∞)上是增函数求出满足条件的m值.
解答 解:由幂函数y=(m2-4m+1)${x}^{{m}^{2}-2m-3}$为(0,+∞)上的增函数,
可得m2-4m+1=1,解得m=4或0;
又幂函数y=${x}^{{m}^{2}-2m-3}$在区间(0,+∞)上是增函数,
∴m2-2m-3>0,
∴m=4时满足条件.
故答案为:4.
点评 本题考查了幂函数的定义与性质的应用问题,是基础题.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
6.设向量$\overrightarrow{a}$,$\overrightarrow{b}$是互相垂直的两个单位向量,且|$\overrightarrow{a}$-3$\overrightarrow{b}$|=m|$\overrightarrow{a}$+$\overrightarrow{b}$|,则实数m的值为( )
| A. | $\sqrt{10}$ | B. | ±$\sqrt{10}$ | C. | $\sqrt{5}$ | D. | ±$\sqrt{5}$ |
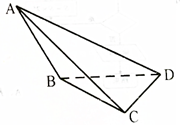 如图所示,在三棱锥A-BCD中,侧面ABD,ACD是全等的直角三角形,AD是公共的斜边且AD=$\sqrt{3}$,BD=CD=1,另一侧面ABC是正三角形.
如图所示,在三棱锥A-BCD中,侧面ABD,ACD是全等的直角三角形,AD是公共的斜边且AD=$\sqrt{3}$,BD=CD=1,另一侧面ABC是正三角形.