题目内容

5．已知a为实数，若复数z=（a2-1）+（a+1）i为纯虚数，则$\frac{{a+{i^{2016}}}}{1+i}$的值为（　　）
A．1B．0C．1+iD．1-i

分析 利用复数是纯虚数求出a，然后利用复数的幂运算以及复数的除法运算法则化简求解即可．

解答 解：复数z=（a2-1）+（a+1）i为纯虚数，可得a=1，
$\frac{{a+{i^{2016}}}}{1+i}$=$\frac{1+1}{1+i}$=$\frac{2（1-i）}{（1+i）（1-i）}$=1-i．
故选：D．

点评 本题考查复数的代数形式混合运算，考查计算能力．

练习册系列答案
相关题目
15．某地市高三理科学生有15000名，在一次调研测试中，数学成绩ξ服从正态分布N（100，σ2），已知p（80＜ξ≤100）=0.35，若按成绩分层抽样的方式取100份试卷进行分析，则应从120分以上的试卷中抽取（　　）
A．5份B．10份C．15份D．20份
16．要从编号为1～50的50名学生中用系统抽样方法抽出5人，所抽取的5名学生的编号可能是（　　）
A．5，10，15，20，25B．3，13，23，33，43C．1，2，3，4，5D．2，4，8，16，32
13．若命题p：?x0∈[-3，3]，x${\;}_{0}^{2}$+2x0+1≤0，则命题p的否定是（　　）
A．?x0∈（-∞，-3）∪（3，+∞），x${\;}_{0}^{2}$+2x0+1≤0B．?x0∈[-3，3]，x${\;}_{0}^{2}$+2x0+1≤0
C．?x∈（-∞，-3）∪（3，+∞），x2+2x+1＞0D．?x∈[-3，3]，x2+2x+1＞0
20．为了解从事微商的人的年龄分布情况，某调查机构所辖市的A，B两个街区中随机抽取了50名微商的年龄进行了调查统计，结果如表：
 年龄段（岁）20～25  25～3030～40 
 A街区 5 x 10
 B街区 510  y
已知从50名微商中随机抽取一名，抽到年龄在30～40的概率为0.3．
（1）求x，y的值，根据表中数计算两个街区年龄在30岁以下从事微商的概率；
（2）为了解这50名微商的工作生活情况，决定按表中描述的六种情况进行分层抽样，从中选取10名作为一个样本进行跟踪采访，然后再从样本中年龄在25～30的人员中随机选取2人接受电视台专访，求接受专访的2人来自不同街区的概率．
10．平面向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°，$\overrightarrow{a}$=（0，3），|$\overrightarrow{b}$|=2，若λ∈R，则|λ$\overrightarrow{a}$-$\overrightarrow{b}$|的最小值是$\sqrt{3}$．
17．若直线2ax+by-1=0（a＞0，b＞0）经过曲线y=cosπx+1（0＜x＜1）的对称中心，则$\frac{2}{a}$+$\frac{1}{b}$的最小值为3+2$\sqrt{2}$．
14．已知定义在R上的偶函数f（x）在x∈[0，+∞）上单调递增，则满足f（2x-1）＜f（$\frac{1}{3}$）的x的取值范围是（　　）
A．（$\frac{1}{3}$，$\frac{2}{3}$）B．（-$\frac{1}{3}$，$\frac{2}{3}$）C．（$\frac{1}{3}$，$\frac{4}{3}$）D．（-$\frac{1}{3}$，$\frac{4}{3}$）
15．如图，正方形ABCD中，M是BC的中点，若$\overrightarrow{AC}$=λ$\overrightarrow{AM}$+μ$\overrightarrow{BD}$，则λ+μ=（　　）
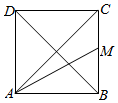
A．$\frac{4}{3}$B．$\frac{5}{3}$C．$\frac{15}{8}$D．2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网