题目内容
14.设函数$f(x)=\left\{\begin{array}{l}3x-1,x<1\\{2^x},x≥1.\end{array}\right.$,则$f(f(\frac{2}{3}))$=2;若f(f(a))=1,则a的值为$\frac{5}{9}$.分析 利用分段函数由里及外逐步求解即可.第二问,通过分类讨论求解方程的解即可.
解答 解:函数$f(x)=\left\{\begin{array}{l}3x-1,x<1\\{2^x},x≥1.\end{array}\right.$,则$f(f(\frac{2}{3}))$=f(3×$\frac{2}{3}-1$)=f(1)=2;
f(f(a))=1,
a<$\frac{2}{3}$时,1=f(3a-1)=3(3a-1)-1,解得a=$\frac{5}{9}$.
当a≥1时,2a>1,f(f(a))=1,不成立;
当$\frac{2}{3}≤a<1$时,f(f(a))=1,23a-1=1,解得a=$\frac{1}{3}$,(舍去).
综上a=$\frac{5}{9}$.
故答案为:$2;\frac{5}{9}$.
点评 本题考查分段函数以及方程根的解法,考查分类讨论思想的应用,是基础题.

练习册系列答案
相关题目
19.实数x,y满足不等式组$\left\{\begin{array}{l}x+y-2≥0\\ x-y-2≤0\\ y≥1\end{array}\right.$则目标函数z=x+2y的最小值是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
3.已知函数f(x)=cos2x+2sinxcosx,则下列说法正确的是( )
| A. | f(x)的图象关于直线$x=\frac{5}{8}π$对称 | |
| B. | f(x)的图象关于点($-\frac{3}{8}π$,0)对称 | |
| C. | 若f(x1)=f(x2),则x1-x2=kπ,k∈Z | |
| D. | f(x)的图象向右平移$\frac{π}{4}$个单位长度后得$g(x)=\sqrt{2}sin(2x+\frac{π}{4})$ |
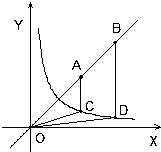 如图,点A、B为直线y=x上的两点,过A、B两点分别作y 轴的平行线交双曲线y=$\frac{1}{x}$(x>0)于C、D两点.若BD=2AC,则4OC2-OD2的值为6.
如图,点A、B为直线y=x上的两点,过A、B两点分别作y 轴的平行线交双曲线y=$\frac{1}{x}$(x>0)于C、D两点.若BD=2AC,则4OC2-OD2的值为6.