题目内容
5.在(2x+a)5的展开式中,含x4项的系数等于160,则${∫}_{0}^{a}$(ex+2x)dx等于( )| A. | e2+3 | B. | e2+4 | C. | e+1 | D. | e+2 |
分析 先二项展开式的通项公式求出a的值,根据积分公式求出即可.
解答 解:由题意可得C5124a=160,
解得a=2,
∴${∫}_{0}^{2}$(ex+2x)dx=(ex+x2)|${\;}_{0}^{2}$=e2+3,
故选:A
点评 本题主要考查二项展开式的应用以及微积分定理的计算,要求熟练掌握相应的计算公式,比较基础.

练习册系列答案
相关题目
16.函数y=cos(2x+φ)(-π≤φ≤π)的图象向右平移$\frac{π}{2}$个单位后与函数$y=sin(2x+\frac{π}{3})$的图象重合,此时φ=( )
| A. | $\frac{5π}{6}$ | B. | $\frac{π}{6}$ | C. | $\frac{2π}{3}$ | D. | $-\frac{π}{6}$ |
20.若sin(${\frac{π}{6}$-α})=$\frac{1}{3}$,则2cos2(${\frac{π}{6}$+$\frac{α}{2}$)-1等于( )
| A. | $\frac{1}{3}$ | B. | $-\frac{1}{3}$ | C. | -$\frac{7}{9}$ | D. | -$\frac{17}{81}$ |
10.若函数f(x)=$\frac{|x-1|}{x+2}$与g(x)=k(x-1)3的图象恰好有两个公共点,则实数k的取值范围是( )
| A. | (-∞,-$\frac{1}{4}$) | B. | (0,+∞) | C. | (-∞,-$\frac{1}{4}$)∪(0,+∞) | D. | (-$\frac{1}{4}$,0) |
5.设函数f(x)是定义在(-∞,0)上的可导函数,其导函数为f'(x),且有2f(x)+xf'(x)>x2,则不等式(x+2017)2f(x+2017)-4f(-2)>0的解集为( )
| A. | (-∞,-2015) | B. | (-∞,-2019) | C. | (-2015,0) | D. | (-2019,0) |
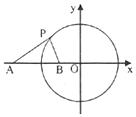 已知圆C:x2+y2=9,点A(-5,0),直线l:x-2y=0.
已知圆C:x2+y2=9,点A(-5,0),直线l:x-2y=0.