题目内容
3.已知函数f(x)=xln|x|+1,则f(x)的极大值与极小值之和为( )| A. | 0 | B. | 1 | C. | $2-\frac{2}{e}$ | D. | 2 |
分析 利用x与0大小讨论,分别求解函数的导数,求解函数的极值,推出结果即可.
解答 解:当x>0时,函数f(x)=xlnx+1,则f′(x)=lnx+1,令lnx+1=0解得x=$\frac{1}{e}$,0<x$<\frac{1}{e}$,f′(x)<0,函数是减函数,当x$>\frac{1}{e}$时,函数是增函数,x=$\frac{1}{e}$函数取得极小值:1-$\frac{1}{e}$;
当x<0时,函数f(x)=xln(-x)+1,则f′(x)=ln(-x)+1,令ln(-x)+1=0解得x=-$\frac{1}{e}$,-$\frac{1}{e}$<x<0,f′(x)<0,函数是减函数,当x$<-\frac{1}{e}$时,函数是增函数,x=-$\frac{1}{e}$函数取得极大值:1+$\frac{1}{e}$;
函数的极值的和为:2.
故选:D.
点评 本题以函数的极值为载体,考查导数在求函数极值的应用,将函数有极大值和极小值,注意分类讨论思想的应用.

练习册系列答案
相关题目
18.据统计,某城市的火车站春运期间日接送旅客人数X(单位:万)服从正态分布X~N(6,0.82),则日接送人数在6万到6.8万之间的概率为( )
(P(|X-μ|<σ)=0.6826,P(|X-μ|<2σ)=0.9544,P(|X-μ|<3σ)=0.9974)
(P(|X-μ|<σ)=0.6826,P(|X-μ|<2σ)=0.9544,P(|X-μ|<3σ)=0.9974)
| A. | 0.6826 | B. | 0.9544 | C. | 0.9974 | D. | 0.3413 |
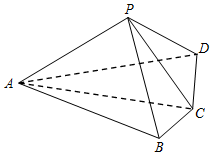 如图,四棱锥P-ABCD中,平面PAC⊥平面ABCD,AC=2BC=2CD=4,∠ACB=∠ACD=60°.
如图,四棱锥P-ABCD中,平面PAC⊥平面ABCD,AC=2BC=2CD=4,∠ACB=∠ACD=60°.
 如图所示的多面体中,底面ABCD为正方形,△GAD为等边三角形,∠GDC=90°,点E是线段GC的中点.
如图所示的多面体中,底面ABCD为正方形,△GAD为等边三角形,∠GDC=90°,点E是线段GC的中点.