题目内容
已知数列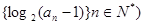 为等差数列,且
为等差数列,且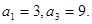
(Ⅰ)求数列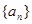 的通项公式;
的通项公式;
(Ⅱ)证明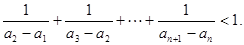
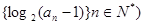 为等差数列,且
为等差数列,且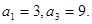
(Ⅰ)求数列
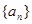 的通项公式;
的通项公式;(Ⅱ)证明
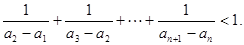
(I)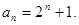 (II)见解析
(II)见解析
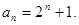 (II)见解析
(II)见解析(I)根据等差数列的通项公式先根据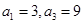 求出数列
求出数列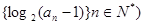
的首项,及公差d,进而可求出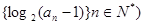 通项公式,所以
通项公式,所以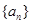 的通项公式得解.
的通项公式得解.
(II)在(I)的基础上,可求出{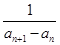 }的通项公式,再根据通项公式的特点有针对性地采用数列求和的方法求和即可
}的通项公式,再根据通项公式的特点有针对性地采用数列求和的方法求和即可
(I)设等差数列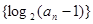 的公差为d.
的公差为d.
由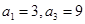 得
得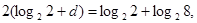 即d=1.
即d=1.
所以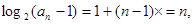 即
即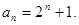
(II)证明: 因为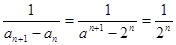 ,
,
所以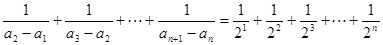
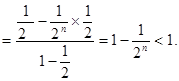
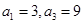 求出数列
求出数列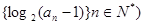
的首项,及公差d,进而可求出
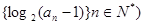 通项公式,所以
通项公式,所以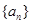 的通项公式得解.
的通项公式得解.(II)在(I)的基础上,可求出{
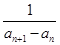 }的通项公式,再根据通项公式的特点有针对性地采用数列求和的方法求和即可
}的通项公式,再根据通项公式的特点有针对性地采用数列求和的方法求和即可(I)设等差数列
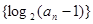 的公差为d.
的公差为d.由
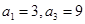 得
得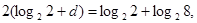 即d=1.
即d=1.所以
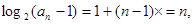 即
即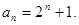
(II)证明: 因为
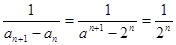 ,
,所以
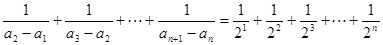
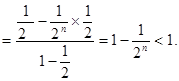

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
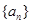 的通项公式为
的通项公式为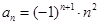 ,其前
,其前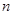 项和为
项和为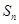 ,
,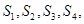 并猜想
并猜想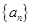 满足
满足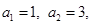
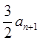 是
是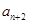 与
与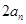 的等差中项
的等差中项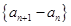 是等比数列;
是等比数列;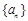 的前n项和为
的前n项和为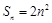 ,
,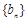 为等比数列,且
为等比数列,且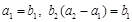 .
.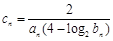 ,求数列
,求数列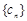 的前n项和
的前n项和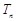 .
.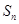 是等差数列
是等差数列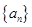 的前
的前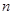 项和,且
项和,且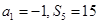 .
.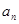 ;
;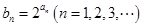 ,计算
,计算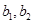 和
和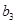 ,由此推测数列
,由此推测数列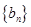 是等差数列还是等比数列,证明你的结论.
是等差数列还是等比数列,证明你的结论.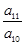 <-1,且它们的前n项和Sn有最大值,则使Sn>0的n的最大值为
<-1,且它们的前n项和Sn有最大值,则使Sn>0的n的最大值为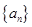 中,
中, ,
,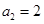 ,
,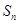 是数列
是数列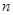 项和,且
项和,且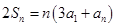 ,
,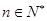 .
. 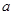 的值;
的值;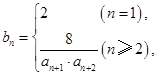
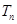 是数列
是数列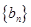 的前
的前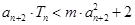 对一切
对一切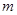 取值范围.
取值范围.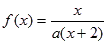 ,方程
,方程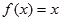 有唯一解,已知
有唯一解,已知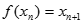
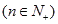 ,且
,且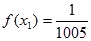 .
.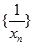 为等差数列,并求数列
为等差数列,并求数列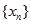 的通项公式;
的通项公式;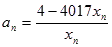 ,且
,且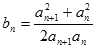
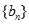 的前
的前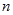 项和
项和 .
.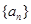 为等差数列,若
为等差数列,若 ,则
,则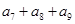 = ( )
= ( )