题目内容
17.若sinα=-$\frac{3}{5}$,α是第三象限的角,则$\frac{cos\frac{α}{2}+sin\frac{α}{2}}{cos\frac{α}{2}-sin\frac{α}{2}}$等于( )| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
分析 由α为第三象限角,根据sinα的值,利用同角三角函数间基本关系求出cosα的值,原式分子分母乘以分子,利用同角三角函数间的基本关系及二倍角的余弦函数公式化简,将各自的值代入计算即可求出值.
解答 解:∵α是第三象限的角,sinα=-$\frac{3}{5}$,
∴cosα=-$\sqrt{1-si{n}^{2}α}$=-$\frac{4}{5}$,
则$\frac{cos\frac{α}{2}+sin\frac{α}{2}}{cos\frac{α}{2}-sin\frac{α}{2}}$=$\frac{(cos\frac{α}{2}+sin\frac{α}{2})^{2}}{co{s}^{2}\frac{α}{2}-si{n}^{2}\frac{α}{2}}$=$\frac{1+sinα}{cosα}$=-$\frac{1}{2}$.
故选:B.
点评 此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
6.已知f(x)是定义在R上的偶函数,且以2为周期,则“f(x)在[0,1]上递增”是“f(x)在[1,2]上递减”的( )
| A. | 既不充分也不必要条件 | B. | 充要条件 | ||
| C. | 必要而不充分条件 | D. | 充分而不必要条件 |

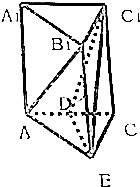
 如图,在四棱台ABCD-A1B1C1D1中,底面ABCD是平行四边形,DD1⊥平面ABCD,AB=$\sqrt{2}$AD,AD=$\sqrt{2}$A1B1,∠BAD=45°.
如图,在四棱台ABCD-A1B1C1D1中,底面ABCD是平行四边形,DD1⊥平面ABCD,AB=$\sqrt{2}$AD,AD=$\sqrt{2}$A1B1,∠BAD=45°. 已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.
已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.