题目内容
5.记max{a1,a2,…an}为a1,a2,…,an中最大的数.已知f(x)=max{x,x2}{-1≤x≤3}(1)求函数y=f(x)的值域;
(2)设P,A,B三点的坐标分别为(x,f(x)),(0,-1),(2,0),且P,A,B三点可以构成三角形,求三角形PAB的面积的取值范围.
分析 (1)将函数y=f(x)的解析式写成分段函数的形式,分段求出函数值的取值范围,综合讨论结果,可得函数y=f(x)的值域;
(2)求出线段AB的长及直线AB的方程,分析出函数图象上的点到直线AB的距离范围,进而可得答案.
解答 解:(1)∵f(x)=max{x,x2}=$\left\{\begin{array}{l}{x}^{2},-1≤x≤0,或1≤x≤3\\ x,0<x<1\end{array}\right.$,
当-1≤x≤0时,f(x)=x2∈[0,1],
当0<x<1时,f(x)=x∈(0,1),
当1≤x≤3,f(x)=x2∈[1,9],
综上所述,函数y=f(x)的值域为[0,9];
(2)∵A,B点的坐标分别为(0,-1),(2,0),
故直线AB所在直线的方程为:$\frac{x}{2}-y=1$,即x-2y-2=0,
且AB=$\sqrt{5}$,
由(1)得:函数y=f(x)图象上的点,(0,0)点距离直线AB最近,
此时三角形PAB的高为$\frac{2}{\sqrt{5}}$,三角形PAB的面积取最小值1,
函数y=f(x)图象上的点,(3,9)点距离直线AB最远,
此时三角形PAB的高为$\frac{17}{\sqrt{5}}$,三角形PAB的面积取最大值$\frac{17}{2}$,
故三角形PAB的面积的取值范围为[1,$\frac{17}{2}$]
点评 本题考查的知识点是分段函数的应用,函数的值域,三角形面积公式,难度中档.

练习册系列答案
相关题目
20.已知随机变量X服从正态分布N(2,σ2),P(X≤3)=0.72,则P(1<X<3)等于( )
| A. | 0.28 | B. | 0.44 | C. | 0.56 | D. | 0.84 |
17.若sinα=-$\frac{3}{5}$,α是第三象限的角,则$\frac{cos\frac{α}{2}+sin\frac{α}{2}}{cos\frac{α}{2}-sin\frac{α}{2}}$等于( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
14.若抛物线y2=mx的准线经过双曲线x2-$\frac{{y}^{2}}{3}$=1的一个焦点,则负数m等于( )
| A. | -1 | B. | -2 | C. | -4 | D. | -8 |
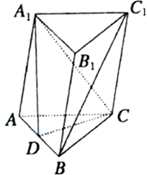 如图所示,在三棱柱ABC-A1B1C1中,AC=BC=BB1,D为AB的中点,求证:BC1∥平面CA1D.
如图所示,在三棱柱ABC-A1B1C1中,AC=BC=BB1,D为AB的中点,求证:BC1∥平面CA1D.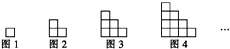 下面图形由小正方形组成,请观察图1至图4的规律,并依此规律,写出第16个图形中小正方形的个数是136.
下面图形由小正方形组成,请观察图1至图4的规律,并依此规律,写出第16个图形中小正方形的个数是136.