题目内容
6.已知f(x)是定义在R上的偶函数,且以2为周期,则“f(x)在[0,1]上递增”是“f(x)在[1,2]上递减”的( )| A. | 既不充分也不必要条件 | B. | 充要条件 | ||
| C. | 必要而不充分条件 | D. | 充分而不必要条件 |
分析 根据充分条件和必要条件的定义结合函数周期性和奇偶性和单调性之间的关系进行判断即可.
解答 解:∵f(x)是定义在R上的偶函数,且以2为周期,则“f(x)在[0,1]上递增,
∴f(x)在[-1,0]上递递减,
则f(x)在[1,2]上递减,
反之若f(x)在[1,2]上递减,
∵函数f(x)是周期为2的周期函数,
∴f(x)在[-1,0]上递递减,
∵f(x)是偶函数,
∴f(x)在[0,1]上递增,
即“f(x)在[0,1]上递增”是“f(x)在[1,2]上递减”的充要条件,
故选:B.
点评 本题主要考查充分条件和必要条件的判断,根据函数奇偶性和周期性与单调性之间的关系是解决本题的关键.

练习册系列答案
相关题目
17.若sinα=-$\frac{3}{5}$,α是第三象限的角,则$\frac{cos\frac{α}{2}+sin\frac{α}{2}}{cos\frac{α}{2}-sin\frac{α}{2}}$等于( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
14.若抛物线y2=mx的准线经过双曲线x2-$\frac{{y}^{2}}{3}$=1的一个焦点,则负数m等于( )
| A. | -1 | B. | -2 | C. | -4 | D. | -8 |
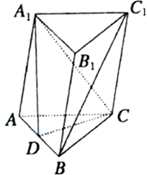 如图所示,在三棱柱ABC-A1B1C1中,AC=BC=BB1,D为AB的中点,求证:BC1∥平面CA1D.
如图所示,在三棱柱ABC-A1B1C1中,AC=BC=BB1,D为AB的中点,求证:BC1∥平面CA1D.
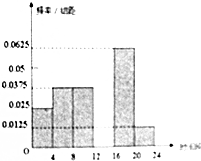 上饶市政府为缓解城市交通压力,计划对金龙岗路等交通要道由双向通行改为单项通行,为调查金龙岗路的通行能力,交警部门将某一天24小时分为六个时段,分别是[0,4)…[20,24)(小时),并记录每一时段通行此路的机动车的辆数,共计为600辆,绘制如下部分频率分布直方图,观察图形的信息,回答下列问题:
上饶市政府为缓解城市交通压力,计划对金龙岗路等交通要道由双向通行改为单项通行,为调查金龙岗路的通行能力,交警部门将某一天24小时分为六个时段,分别是[0,4)…[20,24)(小时),并记录每一时段通行此路的机动车的辆数,共计为600辆,绘制如下部分频率分布直方图,观察图形的信息,回答下列问题: