题目内容
14.已知实数x,y,z满足x+y+z=1,求3x2+2y2+2z2的最小值.分析 利用已知条件x+y+z=1结合柯西不等式,求解3x2+2y2+2z2的最小值.
解答 解:由柯西不等式,${(x+y+z)^2}≤[{{{(\sqrt{3}x)}^2}+{{(\sqrt{2}y)}^2}+{{(\sqrt{2}z)}^2}}]•[{{{(\frac{1}{{\sqrt{3}}})}^2}+{{(\frac{1}{{\sqrt{2}}})}^2}+{{(\frac{1}{{\sqrt{2}}})}^2}}]$,
因为x+y+z=1,所以$3{x^2}+2{y^2}+2{z^2}≥\frac{3}{4}$,
当且仅当$\frac{{\sqrt{3}x}}{{\frac{1}{{\sqrt{3}}}}}=\frac{{\sqrt{2}y}}{{\frac{1}{{\sqrt{2}}}}}=\frac{{\sqrt{2}z}}{{\frac{1}{{\sqrt{2}}}}}$,即$x=\frac{1}{4},y=\frac{3}{8},z=\frac{3}{8}$时,等号成立,
所以3x2+2y2+2z2的最小值为$\frac{3}{4}$…(10分).
点评 本题考查柯西不等式在最值中的应用,考查计算能力.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
4.已知双曲线的一个焦点与抛物线x2=24y的焦点重合,其一条渐近线的倾斜角为60°,则该双曲线的标准方程为( )
| A. | $\frac{x^2}{9}-\frac{y^2}{27}=1$ | B. | $\frac{y^2}{9}-\frac{x^2}{27}=1$ | C. | $\frac{y^2}{27}-\frac{x^2}{9}=1$ | D. | $\frac{x^2}{27}-\frac{y^2}{9}=1$ |
4.下列函数中,值域为[0,+∞)的偶函数是( )
| A. | y=x2+1 | B. | y=lgx | C. | y=|x| | D. | y=xcosx |
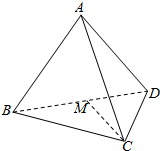 如图,在三棱锥A-BCD中,等边△BCD的边长为4,△ABD是以∠A为直角的等腰直角三角形,平面ABD⊥平面BCD,点M是棱BD的中点.
如图,在三棱锥A-BCD中,等边△BCD的边长为4,△ABD是以∠A为直角的等腰直角三角形,平面ABD⊥平面BCD,点M是棱BD的中点.