题目内容
5．函数y=$\frac{1}{{x}^{4}}$，则y′=-$\frac{4}{{x}^{5}}$．分析 利用复合函数求导法则求出．
解答 解：y′=-$\frac{1}{{x}^{8}}$×4x3=-$\frac{4}{{x}^{5}}$．
故答案为-$\frac{4}{{x}^{5}}$．
点评 本题考查了导数的运算，属于基础题．
练习册系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
15．已知函数f（x）=2sin（ωx+$\frac{π}{3}$）在区间（0，π）上存在唯一一个x0∈（0，π），使得f（x0）=1，则
（ ）
（ ）
| A． | ω的最小值为$\frac{1}{3}$ | B． | ω的最小值为$\frac{1}{2}$ | C． | ω的最大值为$\frac{11}{6}$ | D． | ω的最大值为$\frac{13}{6}$ |
16．
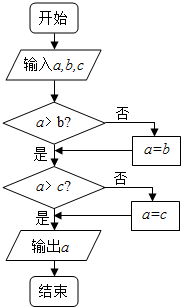已知函数f（x）=2x+x，g（x）=log2x+x，h（x）=log5x+x的零点依次为x1、x2、x3，若在如图所示的算法中，另a=x1，b=x2，c=x3，则输出的结果是（ ）
已知函数f（x）=2x+x，g（x）=log2x+x，h（x）=log5x+x的零点依次为x1、x2、x3，若在如图所示的算法中，另a=x1，b=x2，c=x3，则输出的结果是（ ）| A． | x1 | B． | x2 | C． | x3 | D． | x2或x3 |
13．2015年高考体检中，某校高三共有学生1000人，检查的身体的某项指标为由低到高的4个等级，具体如下表：
（1）若按分层抽样的方法从中抽取20人，再从这20人中抽取2人，求这2人的该项身体指标级别至少有1人小于2人的概率；
（2）若把该校高三学生该项指标中恰好为1级的频率视为概率，从这1000人中任选1人，若其该项指标恰好为1级则结束，否则再选取1人，依次选取，直至找到1人该项指标恰好为1级或选够4人，则结束选取，求结束时选取的人数的分布列与期望．
| 等级 | 1级 | 2级 | 3级 | 4级 |
| 人数 | 200 | 500 | 200 | 100 |
（2）若把该校高三学生该项指标中恰好为1级的频率视为概率，从这1000人中任选1人，若其该项指标恰好为1级则结束，否则再选取1人，依次选取，直至找到1人该项指标恰好为1级或选够4人，则结束选取，求结束时选取的人数的分布列与期望．
14．如果函数f（x）=$\sqrt{x}$在点x=x0处的瞬时变化率是$\frac{\sqrt{3}}{3}$，则x0的值是（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{1}{2}$ | C． | 1 | D． | 3 |