题目内容
1.已知函数f(x)在(-∞,+∞)上是减函数,且f(-1)=e,g(x)=-4x+m•2x+1+m2+2m-1,若M={x|f(g(x))>e}=R,则实数m的取值范围是[-2,0].分析 根据函数单调性的性质将不等式进行转化不等式恒成立问题,构造函数,利用换元法转化为一元二次函数恒成立进行求解即可.
解答 解:∵函数f(x)在(-∞,+∞)上是减函数,且f(-1)=e,
∴不等式f(g(x))>e等价为f(g(x))>f(-1),
即g(x)<-1,
若M={x|f(g(x))>e}=R
则等价为g(x)<-1恒成立,
即-4x+m•2x+1+m2+2m-1<-1,
即-4x+m•2x+1+m2+2m<0恒成立,
设t=2x,则t>0,
则不等式等价为-t2+2mt+m2+2m<0,
即t2-2mt-m2-2m>0,在(0,+∞)上恒成立,
设h(t)=t2-2mt-m2-2m,
①$\left\{\begin{array}{l}{-\frac{-2m}{2}=m≤0}\\{h(0)=-{m}^{2}-2m≥0}\end{array}\right.$,即$\left\{\begin{array}{l}{m≤0}\\{-2≤m≤0}\end{array}\right.$,即-2≤m≤0,
②$\left\{\begin{array}{l}{△=4{m}^{2}+4({m}^{2}+2m)<0}\\{-\frac{-2m}{2}>0}\end{array}\right.$,即$\left\{\begin{array}{l}{{m}^{2}+m<0}\\{m>0}\end{array}\right.$,即$\left\{\begin{array}{l}{-1<m<0}\\{m>0}\end{array}\right.$此时无解,
综上-2≤m≤0,
故答案为:[-2,0].
点评 本题主要考查不等式恒成立问题,根据函数单调性进行转化,利用换元法,构造法转化为一元二次函数问题是解决本题的关键.综合性较强.

 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案| A. | 1+i | B. | 1-i | C. | -i | D. | 3-i |
| A. | 3 | B. | 2 | C. | $\frac{5}{2}$ | D. | -2 |
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{{\sqrt{3}}}{2}$ | D. | -$\frac{1}{2}$ |
| A. | 如果直线l与平面α内无数条直线成异面直线,则l∥α | |
| B. | 如果直线l与平面α内无数条直线平行,则l∥α | |
| C. | 如果直线l与平面α内无数条直线成异面直线,则l?α | |
| D. | 如果一条直线与一个平面平行,则该直线平行于这个平面内的所有直线 | |
| E. | 如果一条直线上有无数个点不在平面内,则这条直线与这个平面平行 |
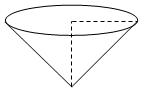 用铁皮制作一个容积为$\frac{1000π}{3}$cm3的无盖圆锥形容器,如图,若圆锥的母线与底面所称的角为45°,求制作该容器需要多少面积的铁皮(铁皮街接部分忽略不计,结果精确到0.1cm2)
用铁皮制作一个容积为$\frac{1000π}{3}$cm3的无盖圆锥形容器,如图,若圆锥的母线与底面所称的角为45°,求制作该容器需要多少面积的铁皮(铁皮街接部分忽略不计,结果精确到0.1cm2)