题目内容
(本小题满分14分)
已知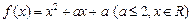 ,
,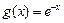 ,
,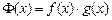 .
.
(1)当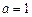 时,求
时,求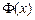 的单调区间;
的单调区间;
(2)求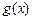 在点
在点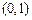 处的切线与直线
处的切线与直线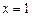 及曲线
及曲线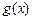 所围成的封闭图形的面积;
所围成的封闭图形的面积;
(3)是否存在实数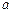 ,使
,使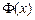 的极大值为3?若存在,求出
的极大值为3?若存在,求出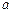 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知
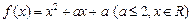 ,
,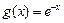 ,
,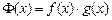 .
.(1)当
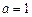 时,求
时,求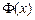 的单调区间;
的单调区间;(2)求
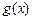 在点
在点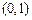 处的切线与直线
处的切线与直线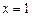 及曲线
及曲线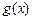 所围成的封闭图形的面积;
所围成的封闭图形的面积;(3)是否存在实数
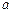 ,使
,使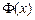 的极大值为3?若存在,求出
的极大值为3?若存在,求出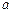 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(1)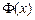 的单调递增区间为(0,1),单调递减区间为:
的单调递增区间为(0,1),单调递减区间为: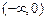 ,
,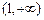
(2)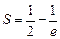 (3)不存在实数
(3)不存在实数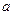 ,使
,使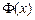 极大值为3
极大值为3
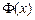 的单调递增区间为(0,1),单调递减区间为:
的单调递增区间为(0,1),单调递减区间为: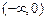 ,
,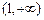
(2)
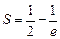 (3)不存在实数
(3)不存在实数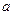 ,使
,使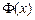 极大值为3
极大值为3解:(1)当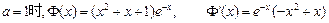 .………1分
.………1分
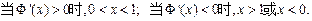 ……………………3分
……………………3分
∴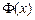 的单调递增区间为(0,1),单调递减区间为:
的单调递增区间为(0,1),单调递减区间为: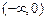 ,
,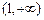 …………4分
…………4分
(2)切线的斜率为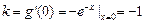 , ∴ 切线方程为
, ∴ 切线方程为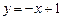 .……………6分
.……………6分
所求封闭图形面积为
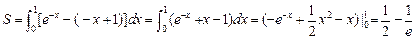 . …………8分
. …………8分
(3)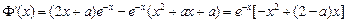 , ………………………9分
, ………………………9分
令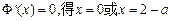 . ………………………………………………………10分
. ………………………………………………………10分
列表如下:
由表可知,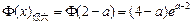 . ………………12分
. ………………12分
设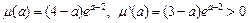 ,
,
∴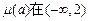 上是增函数,………………………………13分
上是增函数,………………………………13分
∴ ,即
,即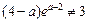 ,
,
∴不存在实数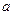 ,使
,使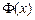 极大值为3. …………………14分
极大值为3. …………………14分
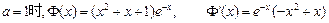 .………1分
.………1分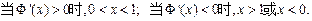 ……………………3分
……………………3分∴
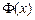 的单调递增区间为(0,1),单调递减区间为:
的单调递增区间为(0,1),单调递减区间为: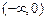 ,
,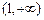 …………4分
…………4分(2)切线的斜率为
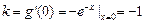 , ∴ 切线方程为
, ∴ 切线方程为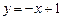 .……………6分
.……………6分 所求封闭图形面积为
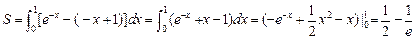 . …………8分
. …………8分(3)
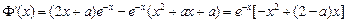 , ………………………9分
, ………………………9分令
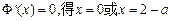 . ………………………………………………………10分
. ………………………………………………………10分列表如下:
| x | (-∞,0) | 0 | (0,2-a) | 2-a | (2-a,+ ∞) |
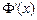 | - | 0 | + | 0 | - |
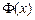 | ↘ | 极小 | ↗ | 极大 | ↘ |
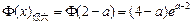 . ………………12分
. ………………12分设
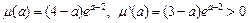 ,
,∴
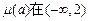 上是增函数,………………………………13分
上是增函数,………………………………13分∴
 ,即
,即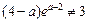 ,
,∴不存在实数
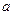 ,使
,使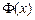 极大值为3. …………………14分
极大值为3. …………………14分
练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时,  (其中e是自然界对数的底,
(其中e是自然界对数的底, )(1)求
)(1)求 ,求证:当
,求证:当 时,
时, ;(3)是否存在实数a,使得当
;(3)是否存在实数a,使得当 时,
时,
 且
且 ,求函数
,求函数 的极大值与极小值.
的极大值与极小值.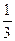 时, 函数取得极大值, 则m的值为 ( )
时, 函数取得极大值, 则m的值为 ( )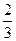
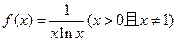
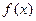 的单调区间;
的单调区间;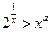 对任意
对任意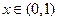 成立,求实数
成立,求实数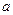 的取值范围。
的取值范围。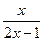 在点(1,1)处的切线方程为( )
在点(1,1)处的切线方程为( )