题目内容
【题目】在直角坐标系中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以原点为极点,
为参数),以原点为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为:
的极坐标方程为:![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)写出曲线![]() 的极坐标方程,并指出它是何种曲线;
的极坐标方程,并指出它是何种曲线;
(Ⅱ)设![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,求四边形
两点,求四边形![]() 面积的取值范围.
面积的取值范围.
【答案】(Ⅰ)![]() ,圆;(Ⅱ)
,圆;(Ⅱ)![]() .
.
【解析】
(Ⅰ)将参数方程化为普通方程,可知曲线![]() 是以
是以![]() 为圆心,
为圆心,![]() 为半径的圆;根据直角坐标与极坐标互化原则可得到曲线
为半径的圆;根据直角坐标与极坐标互化原则可得到曲线![]() 的极坐标方程;(Ⅱ)设
的极坐标方程;(Ⅱ)设![]() ,
,![]() ,联立
,联立![]() 与圆
与圆![]() 方程可得韦达定理的形式;则
方程可得韦达定理的形式;则![]() ,整理可得
,整理可得![]() ,代入
,代入![]() 替换
替换![]() 可求得
可求得![]() ;根据垂直关系可知所求面积为
;根据垂直关系可知所求面积为![]() ,根据三角函数知识可求得结果.
,根据三角函数知识可求得结果.
(Ⅰ)由![]() (
(![]() 为参数)消去参数
为参数)消去参数![]() 得:
得:![]()
将曲线![]() 的方程化成极坐标方程得:
的方程化成极坐标方程得:![]()
![]() 曲线
曲线![]() 是以
是以![]() 为圆心,
为圆心,![]() 为半径的圆
为半径的圆
(Ⅱ)设![]() ,
,![]()
由![]() 与圆
与圆![]() 联立方程得:
联立方程得:![]()
![]() ,
,![]()
![]() 三点共线
三点共线
则![]()
![]() 用
用![]() 代替
代替![]() 可得:
可得:![]()
![]()
![]()
![]()
![]()

练习册系列答案
相关题目
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据
(吨)标准煤的几组对照数据
|
|
|
|
|
|
|
|
|
|
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式: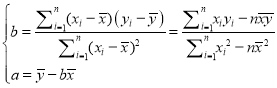
【题目】某中学从高三男生中随机抽取n名学生的身高,将数据整理,得到的频率分布表如表所示:
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.05 |
第2组 |
| a | 0.35 |
第3组 |
| 30 | b |
第4组 |
| 20 | 0.20 |
第5组 |
| 10 | 0.10 |
合计 | n | 1.00 | |
(1)求出频率分布表中![]() 的值,并完成下列频率分布直方图;
的值,并完成下列频率分布直方图;
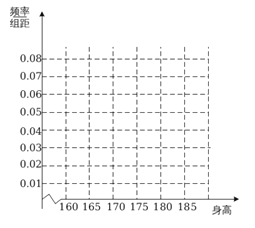
(2)为了能对学生的体能做进一步了解,该校决定在第1,4,5组中用分层抽样取7名学生进行不同项目的体能测试,若在这7名学生中随机抽取2名学生进行引体向上测试,求第4组中至少有一名学生被抽中的概率.
