题目内容
2.已知函数f(x)=$\frac{a}{3}{x^3}-\frac{1}{2}(a+1){x^2}+x-\frac{1}{3}$(a∈R).(1)若a<0,求函数f(x)的极值;
(2)当a≤1时,判断函数f(x)在区间[0,2]上零点的个数.
分析 (1)求出函数的导数,列出表格求出函数的极值即可;
(2)求出函数的导数,通过讨论a的范围,求出函数的单调区间,从而求出函数的零点个数即可.
解答 解:(1)$f'(x)=a{x^2}-(a+1)x+1=a(x-1)(x-\frac{1}{a})$,
∵a<0,∴$\frac{1}{a}<1$
| $(-∞,\frac{1}{a})$ | $\frac{1}{a}$ | $(\frac{1}{a},1)$ | 1 | (1,+∞) | |
| f'(x) | - | 0 | + | 0 | - |
| f(x) | 递减 | 极小值 | 递增 | 极大值 | 递减 |
极大值为$f(1)=-\frac{1}{6}(a-1)$.
(2)由(1)得$f'(x)=a{x^2}-(a+1)x+1=a(x-1)(x-\frac{1}{a})$,
①当a<0时,f(x)在[0,1]上单调递增,在[1,2]上递减.
又因为$f(1)=-\frac{1}{6}(a-1)>0$,$f(0)=-\frac{1}{3}<0$,$f(2)=\frac{1}{3}(2a-1)<0$,
所以f(x)在[0,2]上有两个零点;
②当a=0时,$f(x)=-\frac{1}{2}x+x-\frac{1}{3}$,在[0,2]上有两个零点;
③当$0<a≤\frac{1}{2}$时,$\frac{1}{a}≥2$,f(x)在[0,1]上单调递增,在[1,2]上递减,
又因为$f(1)=-\frac{1}{6}(a-1)>0$,$f(0)=-\frac{1}{3}<0$,$f(2)=\frac{1}{3}(2a-1)≤0$,
所以f(x)在[0,2]上有两个零点;
④当$\frac{1}{2}<a<1$时,$1<\frac{1}{a}<2$,所以f(x)在(0,1)上单调递增,在$(1,\frac{1}{a})$上递减,在$(\frac{1}{a},2)$上递增.
又因为$f(1)=-\frac{1}{6}(a-1)>0$,$f(0)=-\frac{1}{3}<0$,$f(\frac{1}{a})=\frac{{-2{a^2}+3a-1}}{{6{a^2}}}=\frac{-(2a-1)(a-1)}{{6{a^2}}}>0$,
所以f(x)在[0,1]上有且仅有一个零点,在[1,2]上没有零点,
所以f(x)在[0,2]上有且仅有一个零点;
⑤当a=1时,f'(x)≥0恒成立,f(x)在[0,2]单调递增,
∵$f(0)=-\frac{1}{3}<0$,f(2)>0,
所以f(x)在[0,2]上有且仅有一个零点,
综上可知,当$\frac{1}{2}<a≤1$时,f(x)在[0,2]上有且仅有一个零点;
当$a≤\frac{1}{2}$时,f(x)在[0,2]上有两个零点.
点评 本题考查了求函数的单调性、极值问题,考查导数的应用以及函数的零点问题,是一道中档题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
12.已知集合A={-1,1},B={1,2},则A∪B=( )
| A. | ∅ | B. | {-1,1} | C. | {1,2} | D. | {-1,1,2} |
7.三个数0.76,60.7,log0.7 6的大小关系为( )
| A. | log0.7 6<0.7 6<6 0.7 | B. | 0.7 6<6 0.7<log0.7 6 | ||
| C. | log0.7 6<6 0.7<0.76 | D. | 0.7 6<log0.7 6<6 0.7 |
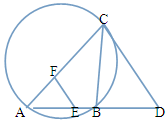 如图,CD为△ABC外接圆的切线,AB的延长线交直线CD与点D,E,F分别为弦AB,AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD与点D,E,F分别为弦AB,AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.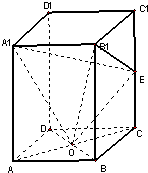 长方体ABCD-A1B1C1D1中,AB=BC=4,AA1=8,E是CC1的中点,O是下底面正方形ABCD的中心.
长方体ABCD-A1B1C1D1中,AB=BC=4,AA1=8,E是CC1的中点,O是下底面正方形ABCD的中心.