题目内容

13．设凸n边形的对角线条数为f（n），若凸n+1边形的对角线条数f（n+1）=f（n）+m，则m的表达式为（　　）
A．n+1B．nC．n-1D．n-2

分析 凸n边形的对角线条数为f（n）=$\frac{1}{2}$n（n-3），进而得到答案．

解答 解：凸n边形的对角线条数为f（n）=$\frac{1}{2}$n（n-3），
∴f（n+1）=$\frac{1}{2}$（n+1）（n+1-3），
若f（n+1）=f（n）+m，
则m=n-1，
故选：C

点评 本题考查的知识点是数列的递推公式，凸n边形对角线公式，难度中档．

练习册系列答案
相关题目
14．已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的离心率为$\frac{2\sqrt{3}}{3}$，其右焦点到直线x=$\frac{{a}^{2}}{c}$的距离为$\frac{1}{2}$，则此双曲线的方程为$\frac{{x}^{2}}{3}-{y}^{2}=1$．
4．点P（x，y）与定点F$（3\sqrt{3}，0）$的距离和它到直线$l：x=4\sqrt{3}$的距离的比是常数$\frac{{\sqrt{3}}}{2}$，
（Ⅰ）求点P的轨迹方程；
（Ⅱ）若直线m与P的轨迹交于不同的两点B、C，当线段BC的中点为M（4，2）时，求直线m的方程．
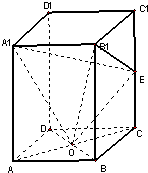1．长方体ABCD-A1B1C1D1中，AB=BC=4，AA1=8，E是CC1的中点，O是下底面正方形ABCD的中心．
（1）求二面角C1-A1B1-O的大小（结果用反三角函数值表示）
（2）求异面直线A1B1与EO所成角的大小（结果用反三角函数值表示）
8．已知集合M={a，b，c}，N={d，e}，则从集合M到N可以建立不同的映射个数为（　　）
A．5B．6C．7D．8
18．如图，在底面是矩形的四棱锥P-ABCD中，PA⊥平面ABCD，PA=AB=2，BC=4，E是PD的中点．
（1）求证：平面PDC⊥平面PAD；
（2）求证：PB∥平面EAC；
（3）求三棱锥E-ACD的体积．
5．某年孝感高中校园歌手大赛后，甲、乙、丙、丁四名同学猜测他们之中谁能获奖．
甲说：“如果我能获奖，那么乙也能获奖．”
乙说：“如果我能获奖，那么丙也能获奖．”
丙说：“如果丁没获奖，那么我也不能获奖．”实际上，他们之中只有一个人没有获奖，并且甲、乙、丙说的话都是真的．那么没能获奖的同学是甲．
2．为了检测某种水果的农药残留，要求这种水果在进入市场前必须对每箱水果进行两轮检测，只有两轮检测都合格水果才能上市销售，否则不能销售．已知每箱这种水果第一轮检测不合格的概率为$\frac{1}{9}$，第二轮检测不合格的概率为$\frac{1}{10}$，每轮检测结果只有“合格”、“不合格”两种，且两轮检测是否合格相互之间没有影响．
（Ⅰ）求每箱水果不能上市销售的概率；
（Ⅱ）如果这种水果可以上市销售，则每箱水果可获利20元；如果这种水果不能上市销售，则每箱水果亏损30元（即获利为-30元）．现有这种水果4箱，记这4箱水果获利的金额为X元，求X的分布列及数学期望．
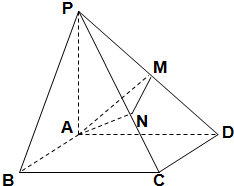3．四棱锥P-ABCD的底面是矩形，PA⊥平面ABCD，且PA=AD=2AB，点M，N分别在侧棱PD，PC上，且$\overrightarrow{PM}=\overrightarrow{MD}$．
（1）求证：平面AMN⊥平面PCD；
（2）若$\overrightarrow{PN}=2\overrightarrow{NC}$，求平面AMN与平面PAB所成锐角的二面角的余弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网