题目内容
18.已知函数f(x)=$\left\{\begin{array}{l}{ln(1-x),x<0}\\{(x-1)^{3}+1,x≥0}\end{array}\right.$,若存在x0,使得f(x0)<ax0成立,则实数a的取值范围是(-∞,0)∪($\frac{3}{4}$,+∞).分析 当a>0时,直线y=ax与y=(x-1)3+1(x≥0)相切,设切点为(m,am),求得x>0的函数的导数,解方程可得m.可得a的值,结合图象可得a的范围;再由a<0,结合图象即可得到所求范围.
解答 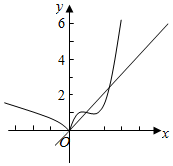 解:当a>0时,直线y=ax与y=(x-1)3+1(x≥0)相切,
解:当a>0时,直线y=ax与y=(x-1)3+1(x≥0)相切,
设切点为(m,am),由y=(x-1)3+1的导数为y′=3(x-1)2,
可得a=3(m-1)2,am=(m-1)3+1,解方程可得m=$\frac{3}{2}$,a=$\frac{3}{4}$.
由图象可得a>$\frac{3}{4}$;
当a<0时,在x<0时,不等式成立.
综上可得a的范围是(-∞,0)∪($\frac{3}{4}$,+∞).
故答案为:(-∞,0)∪($\frac{3}{4}$,+∞).
点评 本题考查不等式成立问题的解法,注意运用数形结合的思想方法,以及导数的运用:求切线的斜率,考查运算能力,属于中档题.

练习册系列答案
相关题目
9.设集合A={x|0≤x≤6},集合B={x|3x2+2x-8≤0},则A∪B=( )
| A. | [0,$\frac{4}{3}$] | B. | [-2,$\frac{4}{3}$] | C. | [0,6] | D. | [-2,6] |