题目内容
下列命题中,正确命题的个数为( )
①“若xy=0,则x=0或y=0”的逆否命题为“若x≠0且y≠0,则xy≠0;
②函数f(x)=ex+x-2的零点所在区间是(1,2);
③x2-5x+6=0是x=2的必要不充分条件.
①“若xy=0,则x=0或y=0”的逆否命题为“若x≠0且y≠0,则xy≠0;
②函数f(x)=ex+x-2的零点所在区间是(1,2);
③x2-5x+6=0是x=2的必要不充分条件.
| A、0 | B、1 | C、2 | D、3 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:①写出“若xy=0,则x=0或y=0”的逆否命题,判断真假即可;
②利用零点存在定理判断函数f(x)=ex+x-2的零点是否在区间是(1,2),即可得到结论;
③利用充要条件判断x2-5x+6=0是x=2的必要不充分条件,得到结果即可.
②利用零点存在定理判断函数f(x)=ex+x-2的零点是否在区间是(1,2),即可得到结论;
③利用充要条件判断x2-5x+6=0是x=2的必要不充分条件,得到结果即可.
解答:
解:①一般地,用p和q分别表示原命题的条件和结论,用¬p或¬q分别表示p和q的否定,则逆否命题为:若¬q则¬p.
由“若xy=0,则x=0或y=0”则逆否命题为:“若x≠0且y≠0,则xy≠0;故本命题正确,
②∵函数f(x)=ex+x-2,∴f(0)=1+0-2=-1<0,f(1)=e+1-2=e-1>0,故有f(0)×f(1)<0,
根据函数零点的判定定理可得函数f(x)=ex+x-2的零点所在区间是(0,1),故本命题不正确.
③x2-5x+6=0成立,则有x=2,或者x=3;故③为假命题.
故选:B.
由“若xy=0,则x=0或y=0”则逆否命题为:“若x≠0且y≠0,则xy≠0;故本命题正确,
②∵函数f(x)=ex+x-2,∴f(0)=1+0-2=-1<0,f(1)=e+1-2=e-1>0,故有f(0)×f(1)<0,
根据函数零点的判定定理可得函数f(x)=ex+x-2的零点所在区间是(0,1),故本命题不正确.
③x2-5x+6=0成立,则有x=2,或者x=3;故③为假命题.
故选:B.
点评:本题主要考察命题的真假判断与应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知直角三角形的周长为定值2l,则它的面积的最大值为( )
A、2
| ||
B、3
| ||
C、(3+2
| ||
D、(3-2
|
在△ABC中,若(
+
)•(
-
)=0,则△ABC为( )
| CA |
| CB |
| CA |
| CB |
| A、正三角形 | B、直角三角形 |
| C、等腰三角形 | D、无法确定 |
已知定义在R上的函数y=f(x)满足下列三个条件:
①对于任意的x∈R,都有f(x+4)=f(x);
②对于任意的0≤x1≤x2≤2,都有f(x1)<f(x2);
③函数y=f(x+2)是偶函数;
则下列结论中正确的是( )
①对于任意的x∈R,都有f(x+4)=f(x);
②对于任意的0≤x1≤x2≤2,都有f(x1)<f(x2);
③函数y=f(x+2)是偶函数;
则下列结论中正确的是( )
| A、f(6.5)<f(5)<f(15.5) |
| B、f(5)<f(6.5)<f(15.5) |
| C、f(5)<f(15.5)<f(6.5) |
| D、f(15.5)<f(5)<f(6.5) |
若?a∈(0,+∞),?θ∈R使asinθ≥a成立,则cos(θ-
)的值为( )
| π |
| 6 |
A、
| ||||
B、
| ||||
C、±
| ||||
D、±
|
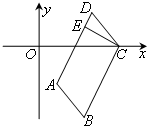 如图,在平行四边形ABCD中,边AD所在直线方程为2x-y-2=0,顶点C(2,0).
如图,在平行四边形ABCD中,边AD所在直线方程为2x-y-2=0,顶点C(2,0).