题目内容
在集合 中,任取一个偶数
中,任取一个偶数 和一个奇数
和一个奇数 ,构成以原点为起点的向量
,构成以原点为起点的向量 .从所有得到的以原点为起点的向量中,任取两个向量为邻边作平行四边形,记所有作成的平行四边形的个数为
.从所有得到的以原点为起点的向量中,任取两个向量为邻边作平行四边形,记所有作成的平行四边形的个数为 ,其中面积等于
,其中面积等于 的平行四边形的个数为
的平行四边形的个数为 ,则
,则 ( )
( )
A. | B. | C. | D. |
B
解析试题分析:因为当 ,
, ,则以
,则以 ,
, 为邻边的平行四边形的面积为
为邻边的平行四边形的面积为

 ,根据条件知平行四边形面积等于
,根据条件知平行四边形面积等于 可转化为
可转化为 (※).由题知以原点为起点的向量
(※).由题知以原点为起点的向量 共有
共有 个,它们分别为
个,它们分别为 、
、
 、
、
 、
、
 、
、
 、
、
 ,因为这
,因为这 个向量任何两个不共线,所以其中任取两个向量为邻边作平行四边形可作
个向量任何两个不共线,所以其中任取两个向量为邻边作平行四边形可作 个,而满足(※)式的向量有
个,而满足(※)式的向量有 和
和 、
、 和
和 、
、 和
和 共
共 对,即
对,即 ,故答案为
,故答案为 .
.
考点:①平行四边形的面积公式;②分步乘法计数原理和分类加法计数原理;③古典概型的概率计算公式.

练习册系列答案
相关题目
从2 004名学生中抽取50名组成参观团,若采用下面的方法选取,先用简单随机抽样从2 004人中剔除4人,剩下的2 000人再按系统抽样的方法进行,则每人入选的概率是( )
| A.不全相等 |
| B.均不相等 |
C.都相等,且为 |
D.都相等,且为 |
对某同学的6次数学测试成绩(满分100分)进行统计,作出的茎叶图如图所示,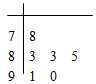
给出关于该同学数学成绩的以下说法:
①中位数为83; ②众数为83; ③平均数为85; ④极差为12.
其中,正确说法的序号是( )
| A.①② | B.②③ | C.③④ | D.②④ |
(本小题满分13分)某幼儿园有教师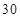 人,对他们进行年龄状况和受教育程度的调查,其结果如下:
人,对他们进行年龄状况和受教育程度的调查,其结果如下:
| | 本科 | 研究生 | 合计 |
| 35岁以下 | 5 | 2 | 7 |
| 35~50岁(含35岁和50岁) | 17 | 3 | 20 |
| 50岁以上 | 2 | 1 | 3 |
(Ⅰ)从该幼儿园教师中随机抽取一人,求具有研究生学历的概率;
(Ⅱ)从幼儿园所有具有研究生学历的教师中随机抽取2人,求有35岁以下的研究生或50岁以上的研究生的概率.
 是虚数单位,则
是虚数单位,则
A. | B. | C. | D. |
若 ,则向量
,则向量 与
与 的夹角为( )
的夹角为( )
A. | B. | C. | D. |
 的焦点
的焦点 且倾斜角为
且倾斜角为 的直线
的直线 与抛物线在第一、四象限分别交于
与抛物线在第一、四象限分别交于 两点,则
两点,则 的值等于( )
的值等于( )

 名
名