题目内容
家政服务公司根据用户满意程度将本公司家政服务员分为两类,其中A类服务员12名,B类服务员 名
名
(1)若采用分层抽样的方法随机抽取20名家政服务员参加技术培训,抽取到B类服务员的人数是16, 求 的值
的值
(2)某客户来公司聘请2名家政服务员,但是由于公司人员安排已经接近饱和,只有3名A类家政服务员和2名B类家政服务员可供选择
①请列出该客户的所有可能选择的情况
②求该客户最终聘请的家政服务员中既有A类又有B类的概率来源:学|科|网]
解: (1)20-16=4, 由 ,可得
,可得 ="48"
="48"
(2) ①设3名A类家政服务员的编号为a,b,c,2名B类家政服务员的编号为1,2,
则所有可能情况有:
(a,b),(a,c),(a,1),(a,2),(b,c),(b,1),(b,2),(c,1),(c,2),(1,2)共10种选择.
②该客户最终聘请的家政服务员中既有A类又有B类的情况有:
(a,1),(a,2),(b,1),(b,2),(c,1),(c,2)共6种选择,  该客户最终聘请的家政服务员中既有A类又有B类的概率为
该客户最终聘请的家政服务员中既有A类又有B类的概率为
解析试题分析:(1)根据分层抽样比例求x的值,
(2)列举出所有的可能,找到满足最终聘请的家政服务员中既有A类又有B类的情况,根据古典概率公式计算即可.
考点:概率与统计.
点评:本题考查了分层抽样和古典概率的问题,关键是一一列举所有的基本事件.

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 是椭圆
是椭圆 的两个焦点,
的两个焦点, 为椭圆上一点,且∠
为椭圆上一点,且∠ ,则
,则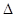
 的面积为( )
的面积为( )
A.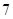 | B. | C.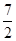 | D. |
如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是( )
| A.62 | B.63 | C.64 | D.56 |
现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片各4张,从中任取3张,要求这三张卡片不能是同一种颜色,且绿色卡片至多1张,不同的取法的种数为
| A.484 | B.472 | C.252 | D.232 |
在 的二项展开式中,常数项为( )
的二项展开式中,常数项为( )
| A.1024 | B.1324 | C.1792 | D.-1080 |
在集合 中,任取一个偶数
中,任取一个偶数 和一个奇数
和一个奇数 ,构成以原点为起点的向量
,构成以原点为起点的向量 .从所有得到的以原点为起点的向量中,任取两个向量为邻边作平行四边形,记所有作成的平行四边形的个数为
.从所有得到的以原点为起点的向量中,任取两个向量为邻边作平行四边形,记所有作成的平行四边形的个数为 ,其中面积等于
,其中面积等于 的平行四边形的个数为
的平行四边形的个数为 ,则
,则 ( )
( )
A. | B. | C. | D. |
设复数 在复平面内的对应点关于虚轴对称,
在复平面内的对应点关于虚轴对称, ,则
,则 =( )
=( )
A. | B. | C. | D. |
 ,众数为
,众数为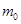 ,平均值为
,平均值为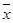 ,则( )
,则( )




 的平均数是
的平均数是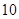 ,标准差是
,标准差是 ,则
,则