题目内容
(本小题满分13分)某幼儿园有教师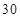 人,对他们进行年龄状况和受教育程度的调查,其结果如下:
人,对他们进行年龄状况和受教育程度的调查,其结果如下:
| | 本科 | 研究生 | 合计 |
| 35岁以下 | 5 | 2 | 7 |
| 35~50岁(含35岁和50岁) | 17 | 3 | 20 |
| 50岁以上 | 2 | 1 | 3 |
(Ⅰ)从该幼儿园教师中随机抽取一人,求具有研究生学历的概率;
(Ⅱ)从幼儿园所有具有研究生学历的教师中随机抽取2人,求有35岁以下的研究生或50岁以上的研究生的概率.
 ,
,
解析试题分析:(Ⅰ)设:“从该幼儿园教师中随机抽取一人,具有研究生学历”为事件 ,
,
由题可知幼儿园总共有教师30人,其中“具有研究生学历”的共6人.
则 .
.
答:从该幼儿园教师中随机抽取一人,具有研究生学历的概率为
(Ⅱ)设幼儿园中35岁以下具有研究生学历的教师为 ,35~50岁(含35岁和50岁)具有研究生学历的教师为
,35~50岁(含35岁和50岁)具有研究生学历的教师为 , 50岁以上具有研究生学历的教师为C,从幼儿园所有具有研究生学历的教师中随机抽取2人,所有可能结果有15个,它们是:
, 50岁以上具有研究生学历的教师为C,从幼儿园所有具有研究生学历的教师中随机抽取2人,所有可能结果有15个,它们是:
( ,
,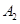 ),(
),( ,
, ),(
),( ,
, ),(
),( ,
, ),(
),( ,C),(
,C),(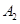 ,
, ),(
),(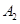 ,
, ),
),
(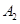 ,
, ),(
),(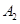 ,C),(
,C),( ,
, ),(
),( ,
, ),(
),( ,C),(
,C),( ,
, ),(
),( ,C),
,C),
( ,C),
,C),
记“从幼儿园所有具有研究生学历的教师中随机抽取2人,有35岁以下的研究生或50岁以上的研究生”为事件 ,则
,则 中的结果共有12个,它们是:(
中的结果共有12个,它们是:( ,
,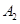 ),(
),( ,
, ),(
),( ,
, ),(
),( ,
, ),(
),( ,C),(
,C),(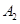 ,
, ),(
),(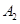 ,
, ),(
),(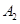 ,
, ),(
),(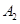 ,C),(
,C),( ,C),(
,C),( ,C),
,C),
( ,C)故所求概率为
,C)故所求概率为 .
.
答:从幼儿园所有具有研究生学历的教师中随机抽取2人,有35岁以下的研究生或50岁以上的研究生的概率为 .
.
考点:本题考查古典概型
点评:将所有的基本事件列出来,从中数出满足题意的基本事件数,两个数值相比

 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案现有16张不同的卡片,其中红色、黄色、蓝色、绿色卡片各4张,从中任取3张,要求这三张卡片不能是同一种颜色,且绿色卡片至多1张,不同的取法的种数为
| A.484 | B.472 | C.252 | D.232 |
在集合 中,任取一个偶数
中,任取一个偶数 和一个奇数
和一个奇数 ,构成以原点为起点的向量
,构成以原点为起点的向量 .从所有得到的以原点为起点的向量中,任取两个向量为邻边作平行四边形,记所有作成的平行四边形的个数为
.从所有得到的以原点为起点的向量中,任取两个向量为邻边作平行四边形,记所有作成的平行四边形的个数为 ,其中面积等于
,其中面积等于 的平行四边形的个数为
的平行四边形的个数为 ,则
,则 ( )
( )
A. | B. | C. | D. |
一个算法的程序框图如图所示,则该程序运行后输出的值是( ).
| A.4 | B.5 | C.6 | D.7 |
已知 是虚数单位,
是虚数单位, 和
和 都是实数,且
都是实数,且 ,则
,则 ( )
( )
A. | B. | C. | D. |
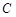 :
: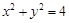 .
.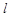 过点
过点 ,且与圆
,且与圆 、
、 两点,若
两点,若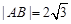 ,求直线
,求直线 的方程;
的方程; 作平行于
作平行于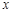 轴的直线
轴的直线 ,设
,设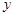 轴的交点为
轴的交点为 ,若向量
,若向量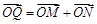 ,求动点
,求动点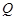 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.



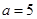 ,则输出的结果是 .
,则输出的结果是 .
 与
与 的夹角为
的夹角为 ,若(
,若( )
) (
( ),则
),则 .
.