题目内容
已知椭圆C的左、右焦点分别为F1,F2,椭圆的离心率为
,且椭圆经过点P(1,
).
(1)求椭圆C的标准方程;
(2)线段PQ是椭圆过点F2的弦,且
=λ
,求△PF1Q内切圆面积最大时实数λ的值.
| 1 |
| 2 |
| 3 |
| 2 |
(1)求椭圆C的标准方程;
(2)线段PQ是椭圆过点F2的弦,且
| PF2 |
| F2Q |
考点:椭圆的应用
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)设椭圆的标准方程,利用椭圆的离心率为
,且椭圆经过点P(1,
),结合a2=b2+c2,求出a2=4,b2=3,从而可求椭圆C的标准方程;
(2)分类讨论,确定当直线PQ与x轴垂直时S△PF1Q最大,进而可求△PF1Q内切圆面积最大时实数λ的值.
| 1 |
| 2 |
| 3 |
| 2 |
(2)分类讨论,确定当直线PQ与x轴垂直时S△PF1Q最大,进而可求△PF1Q内切圆面积最大时实数λ的值.
解答:
解:(1)设椭圆的标准方程为
+
=1(a>b>0),则
∵椭圆的离心率为
,且椭圆经过点P(1,
),
∴
=
,
+
=1,
又a2=b2+c2,
∴a2=4,b2=3,
∴
+
=1…(4分)
(2)显然直线PQ不与x轴重合
当直线PQ与x轴垂直时,|PQ|=3,|F1F2|=2,S△PF1Q=3;…(5分)
当直线PQ不与x轴垂直时,设直线PQ:y=k(x-1),k≠0代入椭圆C的标准方程,
整理,得(3+4k2)y2+6ky-9k2=0,△>0.y1+y2=
,y1•y2=
…(7分)
S△PF1Q=
×|F1F2|×|y1-y2|=…=12
令t=3+4k2,∴t>3,k2=
S△PF1Q=3
,
∵0<
<
∴S△PF1Q∈(0,3)
由上,得S△PF1Q∈(0,3]
∴当直线PQ与x轴垂直时S△PF1Q最大,且最大面积为3 …(10分)
设△PF1Q内切圆半径r,则S=4r≤3,
即rmax=
,此时直线PQ与x轴垂直,△PF1Q内切圆面积最大
∴
=
,λ=1…(12分)
| x2 |
| a2 |
| y2 |
| b2 |
∵椭圆的离心率为
| 1 |
| 2 |
| 3 |
| 2 |
∴
| c |
| a |
| 1 |
| 2 |
| 1 |
| a2 |
(
| ||
| b2 |
又a2=b2+c2,
∴a2=4,b2=3,
∴
| x2 |
| 4 |
| y2 |
| 3 |
(2)显然直线PQ不与x轴重合
当直线PQ与x轴垂直时,|PQ|=3,|F1F2|=2,S△PF1Q=3;…(5分)
当直线PQ不与x轴垂直时,设直线PQ:y=k(x-1),k≠0代入椭圆C的标准方程,
整理,得(3+4k2)y2+6ky-9k2=0,△>0.y1+y2=
| -6k |
| 3+4k2 |
| -9k2 |
| 3+4k2 |
S△PF1Q=
| 1 |
| 2 |
|
令t=3+4k2,∴t>3,k2=
| t-3 |
| 4 |
S△PF1Q=3
-3(
|
∵0<
| 1 |
| t |
| 1 |
| 3 |
由上,得S△PF1Q∈(0,3]
∴当直线PQ与x轴垂直时S△PF1Q最大,且最大面积为3 …(10分)
设△PF1Q内切圆半径r,则S=4r≤3,
即rmax=
| 3 |
| 4 |
∴
| PF2 |
| F2Q |
点评:本题考查椭圆的标准方程与几何性质,考查分类讨论的数学思想,考查三角形面积的计算,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某班级有50名学生,期中考试数学成绩X~N(120,σ2),已知P(X>140)=0.2,则X∈[100,140]的人数为( )
| A、5 | B、10 | C、20 | D、30 |
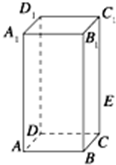 如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.试建立适当的坐标系,写出点B、C、E、A1的坐标.
如图,正四棱柱ABCD-A1B1C1D1中,AA1=2AB=4,点E在CC1上且C1E=3EC.试建立适当的坐标系,写出点B、C、E、A1的坐标.