题目内容
15.某中学组织了一次高二文科学生数学学业水平模拟测试,学校从测试合格的男、女生中各随机抽取100人的成绩进行统计分析,分别制成了如图所示的男生和女生数学成绩的频率分布直方图.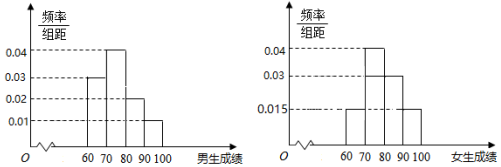
(Ⅰ)若所得分数大于等于80分认定为优秀,求男、女生优秀人数各有多少人?
(Ⅱ)在(Ⅰ)中的优秀学生中用分层抽样的方法抽取5人,从这5人中任意选取2人,求至少有一名男生的概率.
分析 (Ⅰ)根据频率分布直方图求出男、女生优秀人数即可;
(Ⅱ)求出样本中的男生和女生的人数,求出所有的基本事件以及满足条件的基本事件的个数,从而求出满足条件的概率即可.
解答 解:(Ⅰ)由题意可得,男生优秀人数为100×(0.01+0.02)×10=30人,
女生优秀人数为100×(0.015+0.03)×10=45人.
(Ⅱ)因为样本容量与总体中的个体数的比是$\frac{5}{30+45}=\frac{1}{15}$,
所以样本中包含男生人数为$30×\frac{1}{15}=2$人,女生人数为$45×\frac{1}{15}=3$人,
设两名男生为A1,A2,三名女生为B1,B2,B3,
则从5人中任意选取2人构成的所有基本事件为:
{A1,A2},{A1,B1},{A1,B2},{A1,B3},{A2,B1},
{A2,B2},{A2,B3},{B1,B2},{B1,B3},{B2,B3}共10个,
每个样本被抽到的机会均等,因此这些基本事件的出现是等可能的.
记事件C:“选取的2人中至少有一名男生”,
则事件C包含的基本事件有:
{A1,A2},{A1,B1},{A1,B2},{A1,B3},
{A2,B1},{A2,B2},{A2,B3}共7个,
所以$P(C)=\frac{7}{10}$,即选取的2人中至少有一名男生的概率为$\frac{7}{10}$.
点评 本题考查了频率分布问题,考查条件概率问题,是一道中档题.

练习册系列答案
相关题目
6.已知函数f(x)=$\left\{\begin{array}{l}{{e}^{x}-1,x>0}\\{\frac{3}{2}x+1,x≤0}\end{array}\right.$若m<n,且f(m)=f(n),则n-m的取值范围是( )
| A. | [ln2,ln$\frac{3}{2}$+$\frac{1}{3}$] | B. | (ln2,ln$\frac{3}{2}$+$\frac{1}{3}$) | C. | ($\frac{2}{3}$,ln2] | D. | ($\frac{2}{3}$,ln$\frac{3}{2}$+$\frac{1}{3}$] |
10.设随机变量X~N(5,σ2),若P(X>10-a)=0.4,则P(X>a)=( )
| A. | 0.6 | B. | 0.4 | C. | 0.3 | D. | 0.2 |
4.已知f(x)是偶函数,它在[0,+∞)上是减函数,若f(lgx)>f(1),则x的取值范围是( )
| A. | $({\frac{1}{10},1})$ | B. | $({\frac{1}{10},10})$ | C. | $({0,\frac{1}{10}})∪({1,+∞})$ | D. | (0,1)∪(10,+∞) |
5.执行如图程序,输出S的值为( )
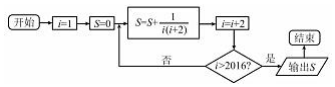

| A. | $\frac{1007}{2015}$ | B. | $\frac{1008}{2017}$ | C. | $\frac{2016}{2017}$ | D. | $\frac{2015}{4032}$ |
 甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中两个阴影部分均为扇形,且每个扇形圆心角均为$\frac{π}{4}$,边界忽略不计)即为中奖.乙商场:从装有2个白球、2个蓝球和2个红球的盒子中一次性摸出1球(这些球除颜色外完全相同),它是红球的概率是$\frac{1}{3}$,若从盒子中一次性摸出2球,且摸到的是2个相同颜色的球,即为中奖.
甲、乙两家商场对同一种商品开展促销活动,对购买该商品的顾客两家商场的奖励方案如下:甲商场:顾客转动如图所示圆盘,当指针指向阴影部分(图中两个阴影部分均为扇形,且每个扇形圆心角均为$\frac{π}{4}$,边界忽略不计)即为中奖.乙商场:从装有2个白球、2个蓝球和2个红球的盒子中一次性摸出1球(这些球除颜色外完全相同),它是红球的概率是$\frac{1}{3}$,若从盒子中一次性摸出2球,且摸到的是2个相同颜色的球,即为中奖.