题目内容
12.若函数y=f(x)是函数y=3x的反函数,则f($\frac{1}{2}$)的值为-log32.分析 利用指数函数的反函数是对数函数,直接求出函数的反函数,然后求出f($\frac{1}{2}$)的值即可.
解答 解:∵指数函数的反函数是对数函数,
∴函数y=3x的反函数为y=f(x)=log3x,
所以f($\frac{1}{2}$)=log3$\frac{1}{2}$=-log32.
故答案为:-log32.
点评 考查了反函数的定义及其性质,属于基础题.

练习册系列答案
相关题目
7.化简$\frac{sin(2π-α)cos(π+α)cos(\frac{π}{2}+α)cos(\frac{11π}{2}-α)}{cos(π-α)sin(3π-α)sin(-π-α)sin(\frac{9π}{2}+α)}$的结果是( )
| A. | 1 | B. | sinα | C. | -tanα | D. | tanα |
17.如图为某几何体的三视图,则该几何体的外接球的表面积为( )
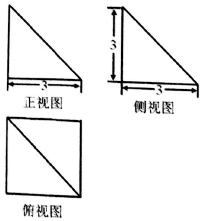

| A. | $\frac{27}{2}π$ | B. | 27π | C. | 27$\sqrt{3}$π | D. | $\frac{27\sqrt{3}π}{2}$ |
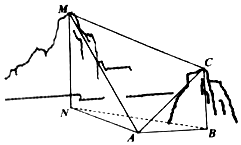 如图,为测量山高l,选择A和另一座山的山顶|PA|为测量观测点.从MB=MC点测得△ABC点的仰角60°,C点的仰角45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,则山高MN=150m.
如图,为测量山高l,选择A和另一座山的山顶|PA|为测量观测点.从MB=MC点测得△ABC点的仰角60°,C点的仰角45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,则山高MN=150m.