题目内容
15.已知a=${∫}_{\frac{1}{e}}^{e}$$\frac{1}{x}$dx,则二项式(1-$\frac{a}{x}$)5的展开式中x-3的系数为( )| A. | 160 | B. | 80 | C. | -80 | D. | -160 |
分析 求定积分可得a的值,再根据二项式展开式的通项公式,求得展开式中x-3的系数.
解答 解:a=${∫}_{\frac{1}{e}}^{e}$$\frac{1}{x}$dx=2,则二项式(1-$\frac{a}{x}$)5 =(1-$\frac{2}{x}$)5 的展开式的通项公式为 Tr+1=${C}_{5}^{r}$•(-2)r•x-r,
令-r=-3,求得r=3,可得展开式中x-3的系数为${C}_{5}^{3}$•(-2)3=-80,
故选:C.
点评 本题主要考查求定积分,二项式定理的应用,二项式展开式的通项公式,属于基础题.

练习册系列答案
相关题目
10.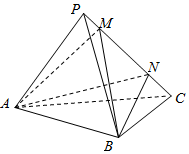 如图,在三棱锥P-ABC中,面PAC⊥面ABC,AB⊥BC,AB=BC=PA=PC=2,M,N为线段PC上的点,若MN=$\sqrt{2}$,则三棱锥A-MNB的体积为( )
如图,在三棱锥P-ABC中,面PAC⊥面ABC,AB⊥BC,AB=BC=PA=PC=2,M,N为线段PC上的点,若MN=$\sqrt{2}$,则三棱锥A-MNB的体积为( )
 如图,在三棱锥P-ABC中,面PAC⊥面ABC,AB⊥BC,AB=BC=PA=PC=2,M,N为线段PC上的点,若MN=$\sqrt{2}$,则三棱锥A-MNB的体积为( )
如图,在三棱锥P-ABC中,面PAC⊥面ABC,AB⊥BC,AB=BC=PA=PC=2,M,N为线段PC上的点,若MN=$\sqrt{2}$,则三棱锥A-MNB的体积为( )| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{1}{3}$ |
20.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F作一条直线,当直线倾斜角为$\frac{π}{6}$时,直线与双曲线左、右两支各有一个交点;当直线倾斜角为$\frac{π}{3}$时,直线与双曲线右支有两个不同的交点,则双曲线离心率的取值范围为( )
| A. | $({1,\frac{{2\sqrt{3}}}{3}})$ | B. | $({\frac{{2\sqrt{3}}}{3},2})$ | C. | $(1,\sqrt{3})$ | D. | (1,2) |
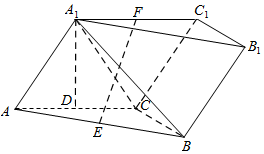 如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,BC=1,且AC⊥BC,点D,E,F分别为AC,AB,A1C1的中点.
如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,BC=1,且AC⊥BC,点D,E,F分别为AC,AB,A1C1的中点.
 某几何体的三视图如图所示,正视图与侧视图完全相同,则该几何体的体积为$\frac{64-8π}{3}$.
某几何体的三视图如图所示,正视图与侧视图完全相同,则该几何体的体积为$\frac{64-8π}{3}$.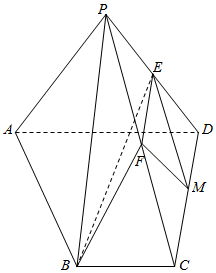 如图所示,已知在四棱锥P-ABCD中,底面四边形ABCD是直角梯形,BC∥AD,BC⊥CD,AD=CD=2BC=4,△PAD是等边三角形,平面PAD⊥平面ABCD,E,F分别是PD,PC的中点,M为CD上一点.
如图所示,已知在四棱锥P-ABCD中,底面四边形ABCD是直角梯形,BC∥AD,BC⊥CD,AD=CD=2BC=4,△PAD是等边三角形,平面PAD⊥平面ABCD,E,F分别是PD,PC的中点,M为CD上一点. 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),圆Q:(x-2)2+(y-$\sqrt{2}$)2=2的圆心Q在椭圆C上,点P(0,$\sqrt{2}$)到椭圆C的右焦点的距离为$\sqrt{6}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),圆Q:(x-2)2+(y-$\sqrt{2}$)2=2的圆心Q在椭圆C上,点P(0,$\sqrt{2}$)到椭圆C的右焦点的距离为$\sqrt{6}$.