题目内容
19.圆O上两点C,D在直径AB的两侧(如图甲),沿直径AB将圆O折起形成一个二面角(如图乙),若∠DOB的平分线交弧$\widehat{BD}$于点G,交弦BD于点E,F为线段BC的中点.
(Ⅰ)证明:平面OGF∥平面CAD.
(Ⅱ)若二面角C-AB-D为直二面角,且AB=2,∠CAB=45°,∠DAB=60°,求四面体FCOG的体积.
分析 (Ⅰ)证明:平面OGF∥平面CAD,只需要证明OG∥平面ACD,证明OG∥AD即可;
(Ⅱ)过G作GH⊥AB,垂足为H,证明线段GH长即为三棱锥G-COF的高,利用V四面体FCOG=V三棱锥G-COF,即可求四面体FCOG的体积.
解答 (Ⅰ)证明:∵OF为△ABC的一条中位线,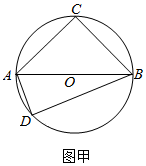
∴OF∥AC.
∵OF?平面ACD,AC?平面ACD,
∴OF∥平面ACD …..…(2分)
∵OG为∠DOB的平分线,∴OG⊥BD.
又可知AD⊥BD,∴OG∥AD…..…(4分)
∵OG?平面ACD,AD?平面ACD,∴OG∥平面ACD…(5分)
∵OG,OF为平面OGF内的两条相交直线,∴平面OGF∥平面CAD…..…(6分)
(Ⅱ)解:过G作GH⊥AB,垂足为H,
又二面角C-AB-D为直二面角,即平面CAB⊥平面DAB.
由已知得O为Rt△ABC斜边AB的中点,∴CO⊥AB,则CO⊥平面DAB,
∴CO⊥GH,∴GH⊥平面CAB,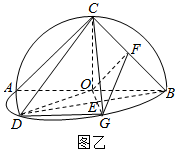
∴线段GH长即为三棱锥G-COF的高…(8分)
又Rt△DAB中,AB=2,∠DAB=60°,∴AD=1,
又OG∥AD,OG=1,OA=1,∴ADGO为菱形,∠AOG=120°,
∴△GOB是边长为1的正三角形,∴GH=$\frac{\sqrt{3}}{2}$…(10分)
又可知△COF为等腰直角三角形,∴${S}_{△COF}=\frac{1}{2}×\frac{\sqrt{2}}{2}×\frac{\sqrt{2}}{2}=\frac{1}{4}$…(11分)
∴V四面体FCOG=V三棱锥G-COF=$\frac{1}{3}×{S}_{△COF}×GH=\frac{\sqrt{3}}{24}$…(12分)
点评 本题考查线线、线面、面面关系,考查面面、线面平行的判定及几何体高与体积的计算,考查空间想象能力、推理论证能力、运算求解能力及分析探究问题和解决问题的能力.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案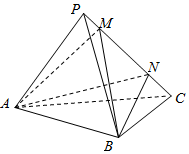 如图,在三棱锥P-ABC中,面PAC⊥面ABC,AB⊥BC,AB=BC=PA=PC=2,M,N为线段PC上的点,若MN=$\sqrt{2}$,则三棱锥A-MNB的体积为( )
如图,在三棱锥P-ABC中,面PAC⊥面ABC,AB⊥BC,AB=BC=PA=PC=2,M,N为线段PC上的点,若MN=$\sqrt{2}$,则三棱锥A-MNB的体积为( )| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{3}$ | D. | $\frac{1}{3}$ |
| A. | 15 | B. | 17 | C. | -15 | D. | -17 |
 如图,已知直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是AA1和CC1的中点,且BE⊥B1F.
如图,已知直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是AA1和CC1的中点,且BE⊥B1F.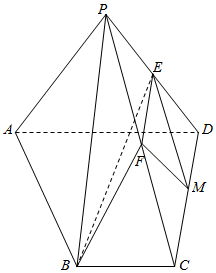 如图所示,已知在四棱锥P-ABCD中,底面四边形ABCD是直角梯形,BC∥AD,BC⊥CD,AD=CD=2BC=4,△PAD是等边三角形,平面PAD⊥平面ABCD,E,F分别是PD,PC的中点,M为CD上一点.
如图所示,已知在四棱锥P-ABCD中,底面四边形ABCD是直角梯形,BC∥AD,BC⊥CD,AD=CD=2BC=4,△PAD是等边三角形,平面PAD⊥平面ABCD,E,F分别是PD,PC的中点,M为CD上一点.