题目内容
已知椭圆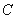 的中心在原点,焦点在
的中心在原点,焦点在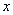 轴上,它的一个顶点恰好经过抛物线
轴上,它的一个顶点恰好经过抛物线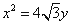 的准线,且经过点
的准线,且经过点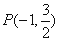 .
.
(Ⅰ)求椭圆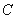 的方程;
的方程;
(Ⅱ) 若直线
若直线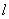 的方程为
的方程为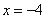 .
.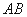 是经过椭圆左焦点
是经过椭圆左焦点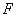 的任一弦,设直线
的任一弦,设直线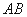 与直线
与直线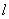 相交于点
相交于点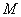 ,记
,记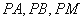 的斜率分别为
的斜率分别为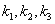 .试探索
.试探索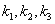 之间有怎样的关系式?给出证明过程.
之间有怎样的关系式?给出证明过程.
解:
(Ⅰ)设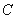 方程为
方程为 ,因为抛物线
,因为抛物线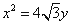 的准线
的准线 ,
, …………1分
…………1分
由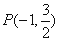 点在椭圆上,
点在椭圆上, ………3分
………3分
∴椭圆C的方程为 . …………4分
. …………4分
(Ⅱ)由题意知,直线斜率存在. 设直线
设直线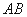 的方程为
的方程为 ,代入
,代入 ,得
,得 , ……5分
, ……5分
设 由韦达定理得
由韦达定理得 . ……6分
. ……6分
由题意知
 ………8分
………8分
 ,代人
,代人 得
得
 ……10分
……10分
 ………12分
………12分
 ………13分
………13分

练习册系列答案
相关题目
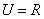 ,集合
,集合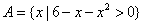 ,集合
,集合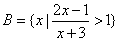
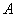 与
与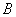 ;
;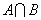 、
、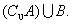
 的左焦点F引圆
的左焦点F引圆 的切线FP交
的切线FP交  的正方体的俯视图是一个面积为
的正方体的俯视图是一个面积为 的正方形,则该正方体的正视图的面积不可能等于
的正方形,则该正方体的正视图的面积不可能等于  B.
B. D.
D.
 的焦点为
的焦点为 两点,若
两点,若 ,则
,则 的焦点为F,准线为
的焦点为F,准线为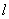 ,P是
,P是 ,则
,则
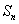 为数列
为数列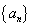 的前
的前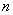 项和,且
项和,且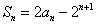 ,n=1,2,3…
,n=1,2,3…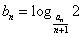 ,数列
,数列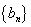 的前
的前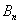 ,若存在整数
,若存在整数 ,使得对任意
,使得对任意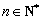 且
且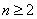
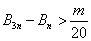 成立,求
成立,求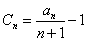 ,证明:
,证明: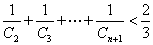 (
(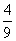 ,乙、丙应聘成功的概率均为
,乙、丙应聘成功的概率均为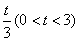 ,且三人是否应聘成功是相互独立的.
,且三人是否应聘成功是相互独立的.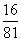 ,求
,求 的值;
的值;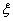 表示甲、乙两人中被聘用的人数,求
表示甲、乙两人中被聘用的人数,求 (
(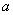 ﹥
﹥ ,
, ﹥
﹥ ,则其渐近线方程为 。
,则其渐近线方程为 。