题目内容
12.设不等式组$\left\{\begin{array}{l}{2x+y≥2}\\{x-2y≥-4}\\{3x-y≤3}\end{array}\right.$所表示的平面区域为M,若z=2x-y+2a+b(a>0,b>0)的最大值为3,则$\frac{1}{a}$+$\frac{1}{b}$的最小值为3$+2\sqrt{2}$.分析 ①画可行域;②z为目标函数的纵截距;③画直线z=x-y.平移可得直线过A或B时z有最值.得到a,b关系式,然后利用基本不等式求解表达式的最小值.
解答 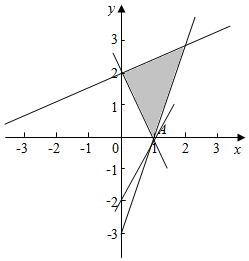 解:画不等式组$\left\{\begin{array}{l}{2x+y≥2}\\{x-2y≥-4}\\{3x-y≤3}\end{array}\right.$所表示的平面区域为M如图,
解:画不等式组$\left\{\begin{array}{l}{2x+y≥2}\\{x-2y≥-4}\\{3x-y≤3}\end{array}\right.$所表示的平面区域为M如图,
画直线z=2x-y+2a+b,
平移直线z=2x-y+2a+b过点A(1,0)时z有最大值3;
则z=2+2a+b=3,解得2a+b=1,a>0,b>0,
则$\frac{1}{a}$+$\frac{1}{b}$=($\frac{1}{a}$+$\frac{1}{b}$)(2a+b)=3+$\frac{2a}{b}$$+\frac{b}{a}$≥3+2$\sqrt{\frac{2a}{b}•\frac{b}{a}}$=3+2$\sqrt{2}$,当且仅当b=$\sqrt{2}a$,2a+b=1,即a=1-$\frac{\sqrt{2}}{2}$,b=$\sqrt{2}-1$时,表达式取得最小值.
故答案为:3+2$\sqrt{2}$.
点评 本题主要考查了简单的线性规划,以及利用几何意义求最值,基本不等式的综合应用,属于中档题.

练习册系列答案
相关题目
2.若复数z=$\frac{2-i}{1+i}$,则|z|=( )
| A. | 1 | B. | $\sqrt{10}$ | C. | $\frac{{\sqrt{10}}}{2}$ | D. | 3 |
1.下列函数为奇函数的是( )
| A. | y=x2 | B. | y=2sinx | C. | y=2cosx | D. | y=2lnx |
12.已知抛物线Γ:y2=2px(p>1)的焦点为F,以F为圆心,2为半径的圆与抛物线的准线交于M,N两点,若△FMN的面积为$\sqrt{3}$,则抛物线Γ的方程为( )
| A. | y2=8x | B. | y2=4$\sqrt{3}$x | C. | y2=4x | D. | y2=2$\sqrt{3}$x |