题目内容
4.已知{an},{bn}均为等比数列,其前n项和分别为Sn,Tn.(1)若a1=8,b2=24,且对任意的n∈N*,总有$\frac{{S}_{n}}{{T}_{n}}$=$\frac{{3}^{n}+1}{4}$,求数列{nan]的前n项和Pn;
(2)当n≤3时,bn-an=n,若数列{an}唯一,求Sn.
分析 (1)通过在$\frac{{S}_{n}}{{T}_{n}}$=$\frac{{3}^{n}+1}{4}$中分别令n=1、2,结合a1=8、b2=24,可得a2=72、b1=8,进而利用错位相减法计算即得结论;
(2)通过bn-an=n(n≤3)整理可知a1q2-4a1q+3a1-1=0,对其根的判别式进行讨论即可.
解答 解:(1)依题意,$\frac{{S}_{1}}{{T}_{1}}$=$\frac{{a}_{1}}{{b}_{1}}$=$\frac{3+1}{4}$=1,$\frac{{S}_{2}}{{T}_{2}}$=$\frac{{a}_{1}+{a}_{2}}{{b}_{1}+{b}_{2}}$=$\frac{{3}^{2}+1}{4}$,
又∵a1=8,b2=24,
∴a2=72,b1=8,
又∵数列{an}、{bn}均为等比数列,
∴an=8•9n-1,bn=8•3n-1,
∴Pn=8(1•1+2•9+3•92+…+n•9n-1),
9Pn=8[1•9+2•92+…+(n-1)•9n-1+n•9n],
两式相减得:-8Pn=8(1+9+92+…+9n-1-n•9n),
∴Pn=n•9n-(1+9+92+…+9n-1)
=n•9n-$\frac{1-{9}^{n}}{1-9}$
=$\frac{1}{8}$+$\frac{8n-1}{8}$•9n;
(2)依题意,b1=1+a1,b2=2+a2,b3=3+a3,
设数列{an}的公比为q,则
(2+a2)2=(1+a1)(3+a3),即(2+a1q)2=(1+a1)(3+a1q2),
整理得:a1q2-4a1q+3a1-1=0,
又∵数列{an}唯一,
∴若上式为完全平方式,则:
当△=$(-4{a}_{1})^{2}$-4a1(3a1-1)=4${{a}_{1}}^{2}$+4a1=0时,
解得:a1=-1(舍)或a1=0(舍);
当△>0,且a1q2-4a1q+3a1-1=0有一个零根和非零根时,
由韦达定理可知:3a1-1=0,即a1=$\frac{1}{3}$,此时q=4;
当△>0且两根都不为零时,但是若有一根可以使bn中有项为0,则与bn为等比数列矛盾,
那么这样的话关于an的方程虽然两根都不为0,但使得bn中有0项的那个根由于与题目矛盾所以必须舍去,
这样an也是唯一的,由此易求出a1=-$\frac{4}{3}$,此时q=$\frac{3}{2}$(舍)或$\frac{5}{2}$;
∴当a1=$\frac{1}{3}$、q=4时,Sn=$\frac{\frac{1}{3}(1-{4}^{n})}{1-4}$=$\frac{{4}^{n}-1}{9}$;
当a1=-$\frac{4}{3}$、q=$\frac{5}{2}$时,Sn=$\frac{-\frac{4}{3}(1-\frac{{5}^{n}}{{2}^{n}})}{1-\frac{5}{2}}$=$\frac{8({2}^{n}-{5}^{n})}{9•{2}^{n}}$.
点评 本题考查数列的通项及前n项和,考查错位相减法,考查运算求解能力,考查分类讨论的思想,注意解题方法的积累,属于难题.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案| A. | ($\frac{1}{3}$,$\frac{2}{3}$) | B. | (-$\frac{1}{3}$,$\frac{2}{3}$) | C. | ($\frac{1}{3}$,$\frac{4}{3}$) | D. | (-$\frac{1}{3}$,$\frac{4}{3}$) |
| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{15}{8}$ | D. | 2 |
| A. | 4200种 | B. | 4320种 | C. | 6120种 | D. | 7920种 |
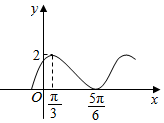 函数f(x)=Asin(ωx-φ)+1(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.
函数f(x)=Asin(ωx-φ)+1(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.