题目内容
函数y=f（x）在（-1，1）上是减函数，且为奇函数，满足f（a2-a-1）+f（a-2）＞0，试 a求的范围．
解：由题意，f（a2-a-1）+f（a-2）＞0，即f（a2-a-1）＞-f（a-2），
又函数y=f（x）为奇函数，所以f（a2-a-1）＞f（2-a），
又函数y=f（x）在（-1，1）上是减函数，
所以有
，?
?1＜a＜
，
所以a的取值范围是（1，）．
分析：根据函数的奇偶性、单调性可把该不等式中的符号“f”去掉，从而变为具体不等式，注意考虑函数的定义域．
点评：本题考查函数的奇偶性、单调性及其应用，考查抽象不等式的求解，解决本题的关键是合理运用函数的性质化抽象不等式为具体不等式．
又函数y=f（x）为奇函数，所以f（a2-a-1）＞f（2-a），
又函数y=f（x）在（-1，1）上是减函数，
所以有
，??1＜a＜，所以a的取值范围是（1，
）．分析：根据函数的奇偶性、单调性可把该不等式中的符号“f”去掉，从而变为具体不等式，注意考虑函数的定义域．
点评：本题考查函数的奇偶性、单调性及其应用，考查抽象不等式的求解，解决本题的关键是合理运用函数的性质化抽象不等式为具体不等式．
练习册系列答案
相关题目
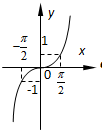已知函数y=f（x）的图象如图，则函数
