题目内容
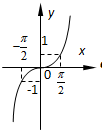 已知函数y=f(x)的图象如图,则函数y=f(
已知函数y=f(x)的图象如图,则函数y=f(| π |
| 2 |
A、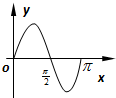 |
B、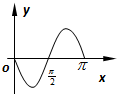 |
C、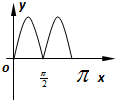 |
D、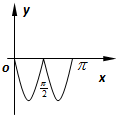 |
分析:先依据f(x)的图象特点,对区间[0,π]上的自变量x进行分类讨论:①当0≤x≤
时;②当
≤x≤π时.研究函数y=f(
-x)•sinx在[0,π]上的函数值的符号,从而即可选出答案.
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
解答:解:当0≤x≤
时,0≤
-x≤
,则函数y=f(
-x)•sinx的值为正;
排除B,D;
当
≤x≤π时,-
≤
-x≤0,则函数y=f(
-x)•sinx的值为负;
排除C;
故选A.
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
排除B,D;
当
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
排除C;
故选A.
点评:华罗庚曾说过:“数缺形时少直观,形缺数时难入微.数形结合百般好,隔离分家万事非.”数形结合是数学解题中常用的思想方法,能够变抽象思维为形象思维,有助于把握数学问题的本质;另外,由于使用了数形结合的方法,很多问题便迎刃而解,且解法简捷.

练习册系列答案
相关题目
 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为 已知函数y=f(x)的图象如图,则满足
已知函数y=f(x)的图象如图,则满足