题目内容
已知函数f(x)=[2sin(x+| π |
| 3 |
| 3 |
(1)求函数f(x)的最小值以及对应的x值.
(2)若函数f(x)关于点(a,0)(a>0)对称,求a的最小值.
(3)做出函数y=f(x)在[0,π]上的图象.
分析:(1)利用两角和的正弦公式及半角公式的变形,化简函数f(x)的解析式,化成关于某个角的正弦.
利用正弦取的最小值的条件求出f(x)的最小值以及对应的x值.
(2)由 2a+
=kπ,求出 a=
kπ-
,故a的最小值
.
(3)利用函数的周期等于π,据五点法作图的步骤,从区间的前端点开始,每隔
个单位取一个点,
得到图象上的五个关键点,然后用平滑的曲线连接.
利用正弦取的最小值的条件求出f(x)的最小值以及对应的x值.
(2)由 2a+
| π |
| 3 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 3 |
(3)利用函数的周期等于π,据五点法作图的步骤,从区间的前端点开始,每隔
| π |
| 4 |
得到图象上的五个关键点,然后用平滑的曲线连接.
解答:解:f(x)=[2sin(x+
)+sinx]cosx-
sin2x=(sinx+
cosx+sinx)cosx-
sin2x
=sin2x+
cos2x=2sin(2x+
)
(1)当且仅当2x+
=2kπ-
,即x=kπ-
(k∈Z)时,f(x)有最小值-2
(2)由已知函数f(x)关于点(a,0)(a>0)对称,
可得 2a+
=kπ,k∈z,所以a=
kπ-
,k∈z.
因为a>0,所以k=1时,a有最小值
.
(3)∵0≤x≤π,∴
≤2x+
≤
,
列表:
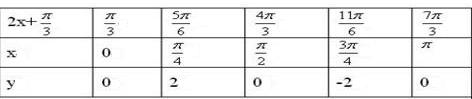
作图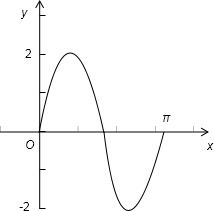
| π |
| 3 |
| 3 |
| 3 |
| 3 |
=sin2x+
| 3 |
| π |
| 3 |
(1)当且仅当2x+
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
(2)由已知函数f(x)关于点(a,0)(a>0)对称,
可得 2a+
| π |
| 3 |
| 1 |
| 2 |
| π |
| 6 |
因为a>0,所以k=1时,a有最小值
| π |
| 3 |
(3)∵0≤x≤π,∴
| π |
| 3 |
| π |
| 3 |
| 7π |
| 3 |
列表:

作图

点评:本题考查两角和差的三角公式的应用,正弦函数的最值及对称中心以及五点法作图的方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|