题目内容
已知
(1)若 的单调递增区间;
的单调递增区间;
(2)若 的最大值为4,求a的值;
的最大值为4,求a的值;
(3)在(2)的条件下,求满足 集合。
集合。
(1) (2)
(2) (3)
(3)
解析试题分析:(1)
令
即
故 的单调递增区间为
的单调递增区间为 4分
4分
(2)
当 8分
8分
(3)
若

即
所以满足条件的 的集合为
的集合为 12分
12分
考点:三角函数化简求值及性质
点评:求三角函数性质首先要将其解析式整理为 的形式,求增区间只需令
的形式,求增区间只需令 求解
求解 的范围,函数的最值由
的范围,函数的最值由 决定
决定

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 cos2ωx+sinωxcosωx+a(其中ω>0,a∈R),且f(x)的图象在y轴右侧的第一个最高点的横坐标为
cos2ωx+sinωxcosωx+a(其中ω>0,a∈R),且f(x)的图象在y轴右侧的第一个最高点的横坐标为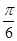 .
.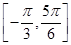 上的最小值为
上的最小值为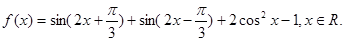 (Ⅰ)求函数
(Ⅰ)求函数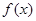 的最小正周期;(Ⅱ)求函数
的最小正周期;(Ⅱ)求函数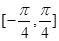 上的最大值和最小值.
上的最大值和最小值.  ,计算:
,计算: ;(2)
;(2) ;(3)
;(3) ;(4)
;(4) ;
;
 ,函数
,函数

 上的值域;
上的值域; 时,若
时,若 与
与 共线,求
共线,求 的值.
的值. 为第三象限角,
为第三象限角, .
. ;
;  ,求
,求 .
.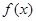 的最小正周期及其单调增区间:
的最小正周期及其单调增区间: 时,求
时,求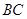 与灯柱
与灯柱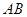 所在平面与道路垂直,且
所在平面与道路垂直,且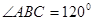 ,路灯
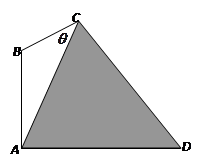
,路灯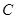 采用锥形灯罩,射出的光线如图阴影部分所示,已知
采用锥形灯罩,射出的光线如图阴影部分所示,已知 ,路宽
,路宽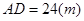 ,设灯柱高
,设灯柱高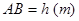 ,
,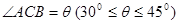 .
.
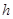 (用
(用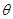 表示);
表示); ,求
,求 ,求
,求 的值;
的值; 为第二象限角,化简
为第二象限角,化简 .
.