题目内容
设函数f(x)= cos2ωx+sinωxcosωx+a(其中ω>0,a∈R),且f(x)的图象在y轴右侧的第一个最高点的横坐标为
cos2ωx+sinωxcosωx+a(其中ω>0,a∈R),且f(x)的图象在y轴右侧的第一个最高点的横坐标为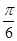 .
.
(1)求ω的值;
(2)如果f(x)在区间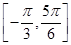 上的最小值为
上的最小值为 ,求a的值.
,求a的值.
(1)ω=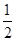 .(2) a=
.(2) a= .
.
解析试题分析:(1)f(x)= cos2ωx+
cos2ωx+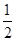 sin2ωx+
sin2ωx+ +a
+a
=sin +
+ +a.
+a.
依题意得2ω·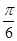 +
+ =
=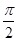 ,解得ω=
,解得ω=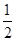 .
.
(2)由(1)知,f(x)=sin +
+ +a.
+a.
又当x∈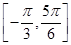 时,x+
时,x+ ∈
∈ ,
,
故 ≤sin
≤sin ≤1,
≤1,
从而f(x)在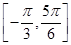 上取得最小值
上取得最小值 +
+ +a.
+a.
由题设知 +
+ +a=
+a= ,故a=
,故a= .
.
考点:和差倍半的三角函数,三角函数的图象和性质。
点评:中档题,本题较为典型,即首先利用和差倍半的三角函数公式,将三角函数式“化一”,进一步研究函数的图像和性质。本题(2)给定了自变量的较小范围,应注意确定 的范围,进一步确定函数的最值。
的范围,进一步确定函数的最值。

练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
 中,
中,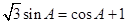 .
. 的大小;
的大小; 的取值范围.
的取值范围.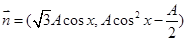 ,
,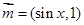 ,
,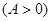 ,函数
,函数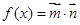 的最大值为
的最大值为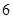 .
.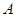 ;
;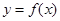 的图像向左平移
的图像向左平移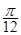 个单位,再将所得图像上各点的横坐标缩短为原来的
个单位,再将所得图像上各点的横坐标缩短为原来的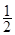 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数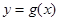 的图像,求
的图像,求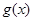 在
在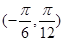 上的值域.
上的值域.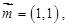 向量
向量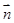 与向量
与向量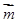 的夹角为
的夹角为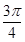 ,且
,且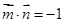 .
.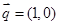 共线,向量
共线,向量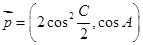 ,其中
,其中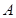 、
、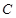 为
为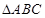 的内角,且
的内角,且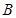 、
、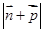 的取值范围.
的取值范围.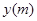 是时间
是时间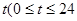 ,单位:
,单位: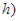 的函数,记作:
的函数,记作: ,下表是该港口在某季每天水深的数据:
,下表是该港口在某季每天水深的数据:
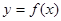 的曲线可以近似地看做函数
的曲线可以近似地看做函数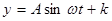 的图象.
的图象. 以上时认为是安全的(船舶停靠时,船底只需不碰到海底即可),某船吃水深度(船底离水面的距离)为
以上时认为是安全的(船舶停靠时,船底只需不碰到海底即可),某船吃水深度(船底离水面的距离)为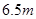 ,如果该船想在同一天内安全进出港,问它至多能在港内停留多长时间(忽略进出港所需时间)?
,如果该船想在同一天内安全进出港,问它至多能在港内停留多长时间(忽略进出港所需时间)? ,
, 在
在 上的最大值与最小值;
上的最大值与最小值; 使得
使得 对任意
对任意 恒成立,求
恒成立,求 的值.
的值. .
. 的最小正周期;
的最小正周期;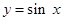 通过怎样的图像变换得到.
通过怎样的图像变换得到. 
 的单调递增区间;
的单调递增区间; 的最大值为4,求a的值;
的最大值为4,求a的值; 集合。
集合。