题目内容
6.规定记号“*”表示一种运算,a*b=a2+ab,设函数f(x)=x*2,且关于x的方程f(x)=ln|x+1|(x≠-1)恰有4个互不相等的实数根x1,x2,x3,x4,则x1+x2+x3+x4=-4.分析 由题意可得f(x)=x2+2x,可得图象关于x=-1对称,由函数图象的变换可得函数y=ln|x+1|(x≠-1)的图象关于直线x=-1对称,进而可得四个根关于直线x=-1对称,由此可得其和.
解答 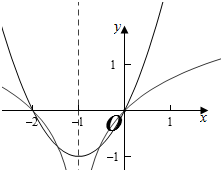 解:由题意可得f(x)=x*2=x2+2x,
解:由题意可得f(x)=x*2=x2+2x,
其图象为开口向上的抛物线,对称轴为x=-1,
函数y=ln|x+1|可由y=ln|x|向左平移1个单位得到,
而函数函数y=ln|x|为偶函数,图象关于y轴对称,
故函数y=ln|x+1|的图象关于直线x=-1对称,
故方程为f(x)=ln|x+1|(x≠-1)四个互不相等的实数根x1,x2,x3,x4,
也关于直线x=-1对称,不妨设x1与x2对称,x3与x4对称,
必有x1+x2=-2,x3+x4=-2,
故x1+x2+x3+x4=-4,
故答案为:-4.
点评 本题考查函数与方程的应用,由新定义得出函数解析式并得出两个函数图象均关于直线x=-1对称是解决问题的关键,利用数形结合比较容易理解.

练习册系列答案
相关题目
16.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-2,x≤0}\\{-lo{g}_{3}x,x>0}\end{array}\right.$,且f(a)=-2,则f(7-a)=( )
| A. | -$\frac{7}{4}$ | B. | -$\frac{5}{4}$ | C. | -$\frac{3}{4}$ | D. | -log37 |
15.若连续抛掷两次骰子得到的点数分别为m,n,则点P(m,n)在函数y=-x+4图象上的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
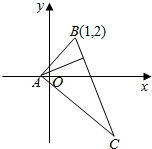 如图,在△ABC中,BC边上的高所在的直线方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0,若点B的坐标为(1,2),求:
如图,在△ABC中,BC边上的高所在的直线方程为x-2y+1=0,∠A的平分线所在的直线方程为y=0,若点B的坐标为(1,2),求: