题目内容
9.在平面直角坐标系中,双曲线C过点P(1,1),且其两条渐近线的方程分别为2x+y=0和2x-y=0,则双曲线C的标准方程为( )| A. | $\frac{x^2}{3}-\frac{{4{y^2}}}{3}=1$ | B. | $\frac{{4{x^2}}}{3}-\frac{y^2}{3}=1$ | ||
| C. | $\frac{{4{x^2}}}{3}-\frac{y^2}{3}=1$或$\frac{x^2}{3}-\frac{{4{y^2}}}{3}=1$ | D. | $\frac{{4{y^2}}}{3}-\frac{x^2}{3}=1$ |
分析 设双曲线C的标准方程为x2-$\frac{{y}^{2}}{4}$=λ,λ≠0,利用待定系数法能求出双曲线C的方程.
解答 解:∵在平面直角坐标系中,双曲线C过点P(1,1),
且其两条渐近线的方程分别为2x+y=0和2x-y=0,
∴设双曲线C的标准方程为x2-$\frac{{y}^{2}}{4}$=λ,λ≠0,
把P(1,1)代入,得:1-$\frac{1}{4}$=λ,解得λ=$\frac{3}{4}$,
∴双曲线C的方程为$\frac{4{x}^{2}}{3}-\frac{{y}^{2}}{3}$=1.
故选:B.
点评 本题考查双曲线的标准方程的求法,是基础题,解题时要认真审题,注意双曲线的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.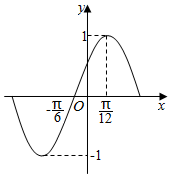 如图是某函数图象的一部分,则该函数表达式是( )
如图是某函数图象的一部分,则该函数表达式是( )
 如图是某函数图象的一部分,则该函数表达式是( )
如图是某函数图象的一部分,则该函数表达式是( )| A. | $y=cos(\frac{π}{6}-2x)$ | B. | $y=cos(2x-\frac{π}{3})$ | C. | $y=sin(x+\frac{π}{6})$ | D. | $y=sin(2x-\frac{π}{6})$ |
4.已知集合A={-1,0,1,2},B={1,x,x2-x},且B⊆A,则x=( )
| A. | 1 | B. | 0 | C. | 2 | D. | -1 |
18.已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}-3x(x≥0)}\\{ln(1-x)(x<0)}\end{array}\right.$,若|f(x)+4|≥a(x-1),则a的取值范围是( )
| A. | [-1,3] | B. | [0,6] | C. | [0,5] | D. | [0,12] |
19.已知函数f(x)=sin(ωx-$\frac{π}{6}$)(ω>0)在区间[-$\frac{π}{2}$,$\frac{4π}{3}$]上单调递增,则实数ω的最大值为( )
| A. | 2 | B. | $\frac{3}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |