题目内容
5.长方体ABCD-A1B1C1D1中,AB=1,AD=2,AA1=3,E为线段A1C上的动点,则满足ED⊥ED1的点E的个数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 无数个 |
分析 以A为坐标原点建立如图所示的空间坐标系,利用向量垂直的充要条件,判断满足条件的点E的个数,进而得到答案.
解答 解:以A为坐标原点建立如图所示的空间坐标系,
则D(0,2,0),D1(0,2,3),
设A1E=λA1C,(0≤λ≤1),
则由A1(0,0,3),$\overrightarrow{{A}_{1}C}$=(1,2,-3)得:
$\overrightarrow{AE}$=(λ,2λ,3-3λ),
则$\overrightarrow{ED}$=(-λ,2-2λ,3λ-3),$\overrightarrow{{ED}_{1}}$=(-λ,2-2λ,3λ),
若ED⊥ED1,则$\overrightarrow{ED}$⊥$\overrightarrow{{ED}_{1}}$,
即λ2+(2-2λ)2+3λ(3λ-3)=0,
即14λ2-17λ+4=0,
解得:λ=$\frac{17±\sqrt{65}}{28}$,
故存在两个满足条件的点,
故选:C.
点评 本题考查的知识点是空间中直线与直线之间的位置关系,向量垂直的充要条件,难度中档.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
16.有下列四个命题:
p1:?x,y∈R,sin(x-y)=sinx-siny;
p2:已知a>0,b>0,若a+b=1,则$\frac{1}{a}+\frac{4}{b}$的最大值是9;
p3:直线ax+y+2a-1=0过定点(0,-l);
p4:曲线y=4x-x3在点(-1,-3)处的切线方程是y=x-2
其中真命题是( )
p1:?x,y∈R,sin(x-y)=sinx-siny;
p2:已知a>0,b>0,若a+b=1,则$\frac{1}{a}+\frac{4}{b}$的最大值是9;
p3:直线ax+y+2a-1=0过定点(0,-l);
p4:曲线y=4x-x3在点(-1,-3)处的切线方程是y=x-2
其中真命题是( )
| A. | p1,p4 | B. | p1p2 | C. | p2,p4 | D. | p3,p4 |
13.已知函数f(x)=$\left\{\begin{array}{l}{ln(x+1),}&{0<x≤2}\\{1-{2}^{x},}&{-2≤x≤0}\end{array}\right.$,若g(x)=|f(x)|-kx-k有3个零点,则实数k的取值范围是( )
| A. | (0,$\frac{1}{e}$) | B. | (0,$\frac{1}{2e}$) | C. | [$\frac{ln3}{3}$,$\frac{1}{2e}$] | D. | [$\frac{ln3}{3}$,$\frac{1}{e}$) |
17.函数f(x)=|lgx|-cosx的零点的个数为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
14.已知命题p:?x∈(1,+∞),$\sqrt{x}$>1;命题q:?a∈(0,1),函数y=ax在(-∞,+∞)上为减函数,则下列命题为真命题的是( )
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | ¬p∧¬q |
 如图是用条件语句编写的一个程序:若输入4,则输出的结果是15,该程序的功能是求函数$y=\left\{{\begin{array}{l}{{x^2}-1}\\ 2\\{2x}\end{array}}\right.,\begin{array}{l}{x>3}\\{x=3}\\{x<3}\end{array}$的值.
如图是用条件语句编写的一个程序:若输入4,则输出的结果是15,该程序的功能是求函数$y=\left\{{\begin{array}{l}{{x^2}-1}\\ 2\\{2x}\end{array}}\right.,\begin{array}{l}{x>3}\\{x=3}\\{x<3}\end{array}$的值.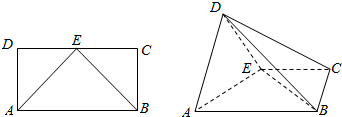 如图,在长方形ABCD中,AB=2,AD=1,E为CD的中点,以AE为折痕,把△DAE折起为△D′AE,且平面D′AE⊥平面ABCE.
如图,在长方形ABCD中,AB=2,AD=1,E为CD的中点,以AE为折痕,把△DAE折起为△D′AE,且平面D′AE⊥平面ABCE.