题目内容

6．盒子中有5个大小形状完全相同的小球，其中黑色小球有3个，标号分别为1，2，3，白色小球有2个，标号分别为1，2．
（Ⅰ）若从盒中任取两个小球，求取出的小球颜色相同且标号之和小于或等于4的概率；
（Ⅱ）若盒子里再放入一个标号为4的红色小球，从中任取两个小球，求取出的两个小球颜色不同且标号之和大于3的概率．

分析 （Ⅰ）设黑色小球为A1，A2，A3，白色小球为B1，B2，利用列举法能求出取出的小球颜色相同且标号之和小于或等于4的概率．
（Ⅱ）设红色小球为C4，利用列举法能求出取出的两个小球颜色不同且标号之和大于3的概率．

解答 解：（Ⅰ）设黑色小球为A1，A2，A3，白色小球为B1，B2，
从盒子中任取两个小球，其一切可能的结果组成的基本事件有：
{A1，A2}，{A1，A3}，{A2，A3}，{A1，B1}，{A1，B2}，{A2，B1}，{A2，B2}，{A3，B1}，{A3，B2}，{B1，B2}，共10个，
根据题意，这些基本事件是等可能的，
事件“取出的小球颜色相同且标号之和小于或等于4”包含的基本事件有：
{A1，A2}，{A1，A3}，{B1，B2}，共3个，
∴取出的小球颜色相同且标号之和小于或等于4的概率p1=$\frac{3}{10}$．
（Ⅱ）设红色小球为C4，从盒子中任取两个小球，其一切可能的结果组成的基本事件有：
{A1，A2}，{A1，A3}，{A2，A3}，{A1，B1}，{A1，B2}，{A2，B1}，{A2，B2}，{A3，B1}，
{A3，B2}，{B1，B2}，{A1，C4}，{A2，C4}，{A3，C4}，{B1，C4}，{B2，C4}，共15个，
根据题意这些基本事件是等可能的，
事件“取出的两个小球颜色不同且标号之和大于3”所包含的基本事件有：
{A1，C4}，{A2，B2}，{A2，C4}，{A3，B1}，{A3，B2}，{A3，C4}，{B1，C4}，{B2，C4}，共8个，
∴取出的两个小球颜色不同且标号之和大于3的概率p2=$\frac{8}{15}$．

点评 本题考查概率的求法，是中档题，解题时要认真审题，注意列举法的合理运用．

练习册系列答案
相关题目
16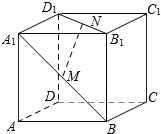．如图，在正方体ABCD-A1B1C1D1中，点M，N分别是面对角线A1B与B1D1的中点，若$\overrightarrow{DA}$=$\overrightarrow{a}$，$\overrightarrow{DC}$=$\overrightarrow{b}$，$\overrightarrow{D{D}_{1}}$=$\overrightarrow{c}$，则$\overrightarrow{MN}$=（　　）
A．$\frac{1}{2}$（$\overrightarrow{c}$+$\overrightarrow{b}$-$\overrightarrow{a}$）B．$\frac{1}{2}$（$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$）C．$\frac{1}{2}$（$\overrightarrow{a}$-$\overrightarrow{c}$）D．$\frac{1}{2}$（$\overrightarrow{c}$-$\overrightarrow{a}$）
17．若不等式a|x|＞x2-$\frac{1}{2}$对任意x∈[-1，1]都成立，则实数a的取值范围是（　　）
A．（$\frac{1}{2}$，1）∪（1，+∞）B．（0，$\frac{1}{2}$）∪（1，+∞）C．（$\frac{1}{2}$，1）∪（1，2）D．（0，$\frac{1}{2}$）∪（1，2）
14．已知数列{an}中，a3=3，an+1=an+2，则a2+a4=6，an=2n-3．
1．某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点，公司为了调查产品销售的情况，需从这600个销售点中，抽取一个容量为100的样本，则应从丙地区中抽取30个销售点．
11．设函数f（x）=1+a•（$\frac{1}{2}$）x+（$\frac{1}{4}$）x，a∈R．
（Ⅰ）不论a为何值时，f（x）不是奇函数；
（Ⅱ）若对任意x∈[0，1]，不等式f（x）≤2016恒成立，求a的取值范围；
（Ⅲ）若f（x）有两个不同的零点，求a的取值范围．
18．已知$\overrightarrow a=（1，5，-1），\overrightarrow b=（-2，3，5）$．
（1）若$（k\overrightarrow a+\overrightarrow b）∥（\overrightarrow a-3\overrightarrow b）$，求实数k的值
（2）若$（k\overrightarrow a+\overrightarrow b）⊥（\overrightarrow a-3\overrightarrow b）$，求实数k的值．
15．某同学在画函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的图象时，列表如下：
x$\frac{2π}{3}$$\frac{5π}{6}$
ωx+φ0$\frac{π}{2}$π$\frac{3π}{2}$2π
Asin（ωx+φ）020-2
（1）请将上表数据补全，并直接写出函数f（x）的解析式；
（2）将函数f（x）图象上各点的纵坐标不变，横坐标缩短为原来的$\frac{1}{2}$，得到函数y=g（x）的图象，求函数y=g（x）在[0，$\frac{π}{2}$]上的最大值M，最小值N，并求M-N的值．
16．一玩具车沿某一斜面自由滑下，测得下滑的水平距离s与时间t之间的函数关系为s=$\frac{1}{2}$t2，则t=3时，此玩具车在水平方向的瞬时速度为（　　）
A．$\frac{3}{2}$B．$\frac{9}{2}$C．2D．3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网