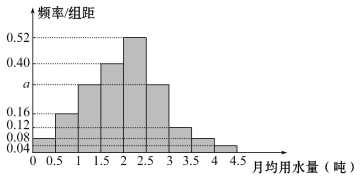
题目内容

【题目】设有半径为的圆形村落， 两人同时从村落中心出发， 向北直行， 先向东直行，出村后不久，改变前进方向，沿着与村落周界相切的直线前进，后来恰与相遇.设两人速度一定，其速度比为，问两人在何处相遇？

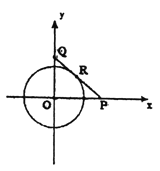
【答案】相遇点在离村中心正北千米处

【解析】试题分析：

由题意建立平面直角坐标系，结合点的坐标和行进的速度可得相遇点在离村中心正北千米处.

试题解析：

如图建立平面直角坐标系，由题意可设两人速度分别为千米/小时， 千米/小时，再设出发小时，在点改变方向，又经过小时，在点处与相遇.则两点坐标为.由知，

，

即.

∵， ∴ ①

将①代入，得.

又已知与圆相切，直线在轴上的截距就是两个相遇的位置.

设直线与圆相切，

则有， ∴.

答： 相遇点在离村中心正北千米处

练习册系列答案
相关题目

【题目】我国是世界上严重缺水的国家，某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟定一个合理的月用水量标准x(吨)，一位居民的月用水量不超过x的部分按平价收费，超出x的部分按议价收费.为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量(单位：吨)，将数据按照，，…，分成9组，制成了如图所示的频率分布直方图.

（1）求直方图中a的值.

（2）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数，并说明理由.

（3）若该市政府希望使85%的居民每月的用水量不超过标准x(吨)，估计x的值，并说明理由.

【题目】已知定义在R上的奇函数满足 ，则( )

A. 1 B. C. 2 D.

【题目】已知点为抛物线：的焦点，抛物线上的点满足(为坐标原点)，且.

（1）求抛物线的方程；

（2）若直线：与抛物线交于不同的两点，是否存在实数及定点，对任意实数，都有？若存在，求出的值及点的坐标；若不存在，请说明理由.

【题目】如图所示，一辆汽车从市出发沿海岸一条直公路以的速度向东匀速行驶，汽车开动时，在市南偏东方向距市且与海岸距离为的海上处有一快艇与汽车同时出发，要把一份稿件送给这辆汽车的司机.

（1）快艇至少以多大的速度行驶才能把稿件送到司机手中？

（2）在（1）的条件下，求快艇以最小速度行驶时的行驶方向与所成的角.

【题目】函数（其中），若函数的图象与轴的任意两个相邻交点间的距离为，且函数的图象过点．

（1）求的解析式；

（2）求的单调增区间：

（3）求在的值域．

【题目】某同学大学毕业后，决定利用所学专业进行自主创业，经过市场调查，生产一小型电子产品需投入固定成本2万元，每生产万件，需另投入流动成本万元，当年产量小于万件时，（万元）；当年产量不小于7万件时，（万元）.已知每件产品售价为6元，假若该同学生产的商品当年能全部售完.

（1）写出年利润（万年）关于年产量（万件）的函数解析式；（注：年利润=年销售收入-固定成本-流动成本）

（2）当年产量约为多少万件时，该同学的这一产品所获年利润最大？最大年利润是多少？

（取）.

【题目】在△ABC中，a，b，c分别为内角A，B，C的对边，且asin B＝－bsin.

(1)求A；

(2)若△ABC的面积S＝c2，求sin C的值．

【题目】选修4-4：坐标系与参数方程

在平面直角坐标系中，直线的参数方程为（为参数，），以坐标原点为极点，以轴正半轴为极轴建立极坐标系，曲线的极坐标方程是.

（1）求直线的普通方程和曲线的直角坐标方程；

（2）已知直线与曲线交于两点，且，求实数的值.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网