Question

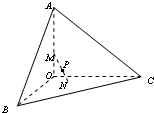已知三棱锥O-ABC，OA、OB、OC两两垂直且长度均为6，长为2的线段MN的一个端点M在棱OA上运动，另一个端点N在△OBC内运动（含边界），则MN的中点P的轨迹与三棱锥的面OAB、OBC、OAC围成的几何体的体积为________．

Answer 1

分析：由于长为2的线段MN的一个端点M在棱OA上运动，另一个端点N在△BCO内运动（含边界），MN的中点P的轨迹为以O为球心，以1为半径的球体，故MN的中点P的轨迹与三棱锥的面所围成的几何体的体积，利用体积分割及球体的体积公式即可．
解答：因为长为2的线段MN的一个端点M在棱OA上运动，另一个端点N在△BCO内运动（含边界），
可知MN的中点P的轨迹为以O为球心，以1为半径的球体，
则MN的中点P的轨迹与三棱锥的面所围成的几何体可能为该球体的，即：V=×π×1³=．
故答案为：．
点评：此题考查了学生的空间想象能力，还考查了球体，三棱锥的体积公式即计算能力．