题目内容
(Ⅰ)设函数 ,证明:当x>0时,f(x)>0.
,证明:当x>0时,f(x)>0.(Ⅱ)从编号1到100的100张卡片中每次随机抽取一张,然后放回,用这种方式连续抽取20次,设抽到的20个号码互不相同的概率为p,证明:
 .
.
【答案】分析:(Ⅰ)欲证明当x>0时,f(x)>0,由于f(0)=0利用函数的单调性,只须证明f(x)在[0,+∞)上是单调增函数即可.先对函数进行求导,根据导函数大于0时原函数单调递减即可得到答案.
(Ⅱ)先计算概率P=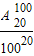 ,再证明
,再证明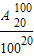
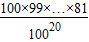
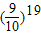
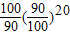 ,即证明99×98×…×81<(90)19,最后证明
,即证明99×98×…×81<(90)19,最后证明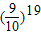 <e-2,即证
<e-2,即证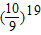 >e2,即证19ln
>e2,即证19ln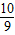 >2,即证ln
>2,即证ln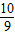
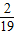 ,而这个结论由(1)所得结论可得
,而这个结论由(1)所得结论可得
解答:(Ⅰ)证明:∵f′(x)=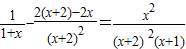 ,
,
∴当x>-1,时f′(x)≥0,
∴f(x)在(-1,+∞)上是单调增函数,
∴当x>0时,f(x)>f(0)=0.
即当x>0时,f(x)>0.
(Ⅱ)从编号1到100的100张卡片中每次随机抽取一张,然后放回,连续抽取20次,则抽得的20个号码互不相同的概率为P=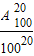 ,要证P<
,要证P<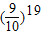 <
<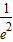 .
.
先证:P= <
< ,即证
,即证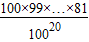 <
<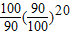
即证99×98×…×81<(90)19
而99×81=(90+9)×(90-9)=902-92<902
98×82=(90+8)×(90-8)=902-82<902…
91×89=(90+1)×(90-1)=902-12<902
∴99×98×…×81<(90)19
即P<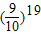
再证: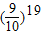 <e-2,即证
<e-2,即证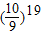 >e2,即证19ln
>e2,即证19ln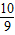 >2,即证ln
>2,即证ln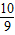 >
>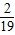
由(Ⅰ)f(x)=ln(1+x)-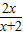 ,当x>0时,f(x)>0.
,当x>0时,f(x)>0.
令x= ,则ln(1+
,则ln(1+ )-
)- =ln(1+
=ln(1+ )-
)-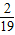 >0,即ln
>0,即ln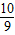 >
>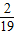
综上有:P<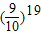 <
<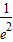
点评:本题主要考查函数单调性的应用、函数的单调性与导数的关系等,考查运算求解能力,函数、导数、不等式证明及等可能事件的概率等知识.通过运用导数知识解决函数、不等式问题,考查了考生综合运用数学知识解决问题的能力.
(Ⅱ)先计算概率P=
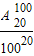 ,再证明
,再证明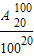
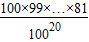
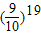
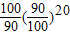 ,即证明99×98×…×81<(90)19,最后证明
,即证明99×98×…×81<(90)19,最后证明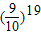 <e-2,即证
<e-2,即证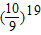 >e2,即证19ln
>e2,即证19ln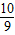 >2,即证ln
>2,即证ln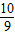
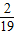 ,而这个结论由(1)所得结论可得
,而这个结论由(1)所得结论可得解答:(Ⅰ)证明:∵f′(x)=
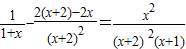 ,
,∴当x>-1,时f′(x)≥0,
∴f(x)在(-1,+∞)上是单调增函数,
∴当x>0时,f(x)>f(0)=0.
即当x>0时,f(x)>0.
(Ⅱ)从编号1到100的100张卡片中每次随机抽取一张,然后放回,连续抽取20次,则抽得的20个号码互不相同的概率为P=
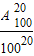 ,要证P<
,要证P<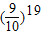 <
<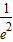 .
.先证:P=
 <
< ,即证
,即证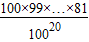 <
<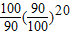
即证99×98×…×81<(90)19
而99×81=(90+9)×(90-9)=902-92<902
98×82=(90+8)×(90-8)=902-82<902…
91×89=(90+1)×(90-1)=902-12<902
∴99×98×…×81<(90)19
即P<
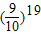
再证:
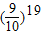 <e-2,即证
<e-2,即证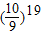 >e2,即证19ln
>e2,即证19ln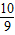 >2,即证ln
>2,即证ln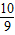 >
>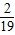
由(Ⅰ)f(x)=ln(1+x)-
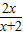 ,当x>0时,f(x)>0.
,当x>0时,f(x)>0.令x=
 ,则ln(1+
,则ln(1+ )-
)- =ln(1+
=ln(1+ )-
)-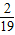 >0,即ln
>0,即ln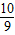 >
>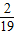
综上有:P<
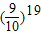 <
<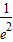
点评:本题主要考查函数单调性的应用、函数的单调性与导数的关系等,考查运算求解能力,函数、导数、不等式证明及等可能事件的概率等知识.通过运用导数知识解决函数、不等式问题,考查了考生综合运用数学知识解决问题的能力.

练习册系列答案
相关题目
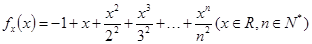 ,证明:
,证明: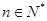 ,存在唯一的
,存在唯一的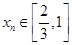 ,满足
,满足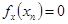 ;
;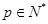 ,由(Ⅰ)中
,由(Ⅰ)中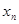 构成的数列
构成的数列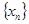 满足
满足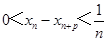 .
.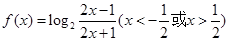 .
. 是奇函数;
是奇函数;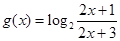 图象的一个对称中心.
图象的一个对称中心.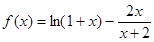 ,证明:当
,证明:当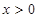 时,
时,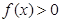 ;
;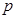 。证明:
。证明: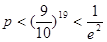 。
。