题目内容
设函数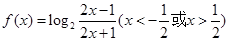 .
.
(1)证明: 是奇函数;
是奇函数;
(2)求 的单调区间;
的单调区间;
(3)写出函数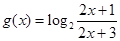 图象的一个对称中心.
图象的一个对称中心.
【答案】
(1) 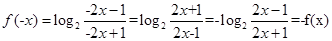 (2) 单调增区间有
(2) 单调增区间有 ; (3)
; (3) 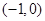 。
。
【解析】
试题分析:(1)易知函数的定义域为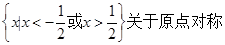 ,
,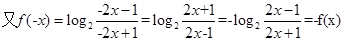 ,所以
,所以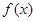 是奇函数。………4分
是奇函数。………4分
(2)令
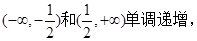 又
又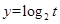 也为单调递增函数,所以函数
也为单调递增函数,所以函数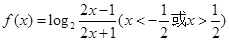 单调增区间有
单调增区间有 。……………………6分
。……………………6分
(3)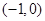 4分
4分
考点:函数的奇偶性;函数的单调性;函数的对称性。
点评:(1)本题主要考查函数性质的综合应用。属于基础题型。(2)判断函数的奇偶性有两步:一求函数的定义域,看定义域是否关于原点对称;二判断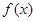 与
与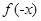 的关系。若定义域不关于原点对称,则函数一定是非奇非偶函数。(3)复合函数的单调性的判断只需用四个字:同增异减。
的关系。若定义域不关于原点对称,则函数一定是非奇非偶函数。(3)复合函数的单调性的判断只需用四个字:同增异减。

练习册系列答案
相关题目
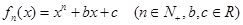
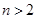 ,
,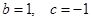 ,证明:
,证明: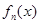 在区间
在区间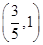 内存在唯一的零点;
内存在唯一的零点; 为偶数,
为偶数,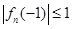 ,
,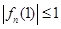 ,求
,求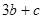 的最小值和最大值;
的最小值和最大值;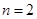 ,若对任意
,若对任意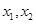
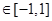 ,有
,有 ,求
,求 的取值范围;
的取值范围;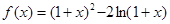
 在
在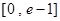 有实数解,求实数m的取值范围;
有实数解,求实数m的取值范围; ,若关于x的方程
,若关于x的方程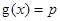 至少有一个解,求p 的最小值.
至少有一个解,求p 的最小值.
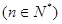
 .
. 的奇偶性;
的奇偶性; 上增减性,并进行证明;
上增减性,并进行证明; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数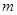 的取值范围.
的取值范围.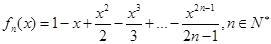
 的单调性;
的单调性;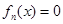 的实数解的个数,并加以证明.
的实数解的个数,并加以证明.