题目内容
(04年广东卷)(12分)
设函数![]()
(I)证明:当![]() 且
且![]() 时,
时,![]()
(II)点![]() (0<x0<1)在曲线
(0<x0<1)在曲线![]() 上,求曲线上在点
上,求曲线上在点![]() 处的切线与
处的切线与![]() 轴,
轴,![]() 轴正向所围成的三角形面积的表达式。(用
轴正向所围成的三角形面积的表达式。(用![]() 表示)
表示)
解析:证明:(I)

故f(x)在(0,1![]() 上是减函数,而在(1,+∞)上是增函数,由0<a<b且f(a)=f(b)得0<a<1<b和
上是减函数,而在(1,+∞)上是增函数,由0<a<b且f(a)=f(b)得0<a<1<b和![]()
故![]()
(II)0<x<1时,
曲线y=f(x)在点P(x0,y0)处的切线方程为:

∴切线与x轴、y轴正向的交点为![]()
故所求三角形面积听表达式为:
![]()

练习册系列答案
相关题目
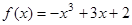 分别在
分别在 、
、 处取得极小值、极大值.
处取得极小值、极大值. 平面上点A、B的坐标分别为
平面上点A、B的坐标分别为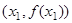 、
、 ,该平面上动点P满足
,该平面上动点P满足 ,点Q是点P关于直线
,点Q是点P关于直线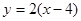 的对称点
的对称点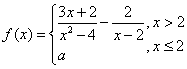 在
在