题目内容
9.以下是某地搜集到的新房屋的销售价格y和房屋的面积x的数据| 房屋面积(平方米) | 115 | 110 | 80 | 135 | 105 |
| 销售价格(万元) | 24.8 | 21.6 | 18.4 | 29.2 | 22 |
(2)求线性回归方程
(3)根据(2)的结果估计房屋面积为150平方米时的销售价格.
分析 (1)根据表中的数据,画出散点图如下;
(2)求出$\overline{x}$、$\overline{y}$,根据回归直线过样本中心点,求出回归系数a、b即可写出回归方程;
(3)根据上一问求出的线性回归方程,代入x=150计算函数的值即可.
解答 解:(1)根据表中的数据,画出散点图如下;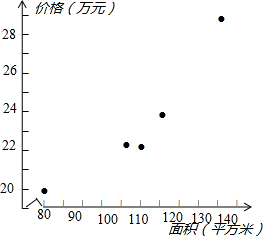
(2)计算$\overline{x}$=$\frac{1}{5}$×(115+110+80+135+105)=109,
$\overline{y}$=$\frac{1}{5}$×(24.8+21.6+18.4+29.2+22)=23.2.
=145,
设所求回归直线方程为$\stackrel{∧}{y}$=bx+a,则
b=$\frac{\sum_{i=1}^{5}{(x}_{i}-\overline{x}){(y}_{i}-\overline{y})}{{\sum_{i=1}^{5}{(x}_{i}-\overline{x})}^{2}}$=$\frac{308}{1570}$≈0.2,
∴a=$\overline{y}$-b$\overline{x}$=23.2-109×0.2≈1.4.
∴所求回归直线方程为$\stackrel{∧}{y}$=0.2x+1.4.
(3)由第(2)问可知,当x=150m2时,
销售价格的估计值为
$\stackrel{∧}{y}$=0.2×150+1.4=31.4(万元).
点评 本题考查了画散点图与求回归直线的方程的应用问题,关键是求回归直线方程的系数,是综合性题目.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
20.函数f(x)=$\frac{1}{3}$ax3+$\frac{1}{2}$ax2-2ax+2a+1的图象经过四个象限的一个充分但不必要条件是( )
| A. | -$\frac{4}{3}$<a<-$\frac{1}{3}$ | B. | -1<a<-$\frac{1}{2}$ | C. | -$\frac{6}{5}$<a<-$\frac{3}{16}$ | D. | -2<a<0 |
4.已知f(x)=$\left\{\begin{array}{l}-{x^2}+3x(x<2)\\ 2x-1(x≥2)\end{array}$,则f(-1)+f(4)的值为( )
| A. | -7 | B. | -8 | C. | 3 | D. | 4 |
5.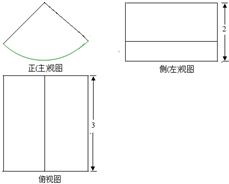 将一个质地均匀的几何体放置在水平面上,其三视图如图所示,其中正(主)视图是一个圆心角为90°的扇形,则该几何体的表面积为( )
将一个质地均匀的几何体放置在水平面上,其三视图如图所示,其中正(主)视图是一个圆心角为90°的扇形,则该几何体的表面积为( )
 将一个质地均匀的几何体放置在水平面上,其三视图如图所示,其中正(主)视图是一个圆心角为90°的扇形,则该几何体的表面积为( )
将一个质地均匀的几何体放置在水平面上,其三视图如图所示,其中正(主)视图是一个圆心角为90°的扇形,则该几何体的表面积为( )| A. | 3π+6 | B. | 5π+6 | C. | 3π+12 | D. | 5π+12 |
12.下列特称命题中假命题为( )
| A. | 空间中过直线外一点有且仅有一条直线与该直线垂直 | |
| B. | 仅存在一个实数b2,使得-9,b1,b2,b3,-1成等比数列 | |
| C. | 存在实数a,b满足a+b=2,使得3a+3b的最小值是6 | |
| D. | ?a∈(-4,0],ax2+ax-1<0恒成立 |
10.已知函数f(x)=(2ax-lnx)x有两个极值点,则实数a的取值范围是( )
| A. | (0,$\frac{1}{4}$) | B. | (0,$\frac{1}{2}$) | C. | (0,1) | D. | (0,+∞) |